Giáo án điện tử Toán 12 kết nối Bài 15: Phương trình đường thẳng trong không gian

CHÀO MỪNG CÁC EM ĐẾN VỚI BÀI GIẢNG HÔM NAY

KHỞI ĐỘNG

Trong không gian , mắt một người quan sát ở điểm và vật cần quan sát đặt tại điểm . Một tấm bìa chắn đường truyền của ánh sáng có dạng hình tròn với tâm bán kính bằng 3 và đặt trong mặt phẳng

Hỏi tấm bìa có che khuất tầm nhìn của người quan sát đối với vật đặt ở điểm hay không?

BÀI 15: PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN

NỘI DUNG BÀI HỌC

Phương trình đường thẳng

2

Hai đường thẳng vuông góc

3

Vị trí tương đối giữa hai đường thẳng

1

1. PHƯƠNG TRÌNH ĐƯỜNG THẲNG

• HĐ1. Hình thành khái niệm vectơ chỉ phương của đường thẳng

a) Có duy nhất đường thẳng đi qua và vuông góc với giá của .

b) Có duy nhất đường thẳng đi qua và song song hoặc trùng với giá của .

a) Vectơ chỉ phương của đường thẳng

KẾT LUẬN

Vectơ được gọi là vectơ chỉ phương của đường thẳng nếu giá của song song hoặc trùng với .

KẾT LUẬN

Vectơ được gọi là vectơ chỉ phương của đường thẳng nếu giá của song song hoặc trùng với .

Chú ý

• Đường thẳng hoàn toàn xác định khi biết một điểm mà nó đi qua và một vectơ chỉ phương.
• Nếu là một vectơ chỉ phương của thì (với là một số khác 0) cũng là một vectơ chỉ phương của .

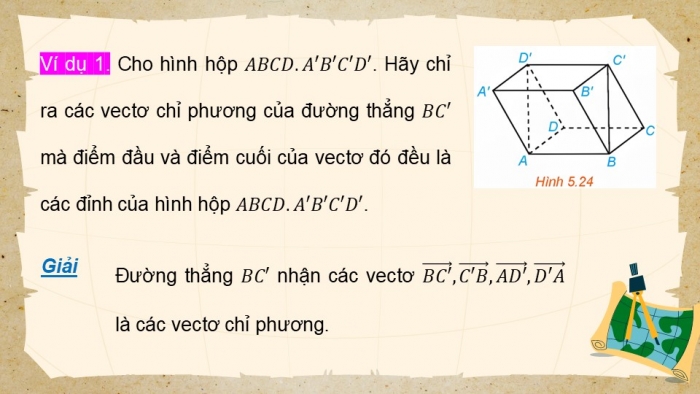
Ví dụ 1. Cho hình hộp . Hãy chỉ ra các vectơ chỉ phương của đường thẳng mà điểm đầu và điểm cuối của vectơ đó đều là các đỉnh của hình hộp .

Đường thẳng nhận các vectơ là các vectơ chỉ phương.

Giải

Cho hình lăng trụ (H.5.25). Trong các vectơ có điểm đầu và điểm cuối đều là đỉnh của hình lăng trụ, những vectơ nào là vectơ chỉ phương của đường thẳng ?

Giải

Những vectơ chỉ phương của đường thẳng là .

Luyện tập 1

• HĐ2. Hình thành khái niệm phương trình tham số của đường thẳng

b) Phương trình tham số của đường thẳng.

a) Hỏi vật thể chuyển động trên đường thẳng nào (chỉ ra điểm mà nó đi qua và vectơ chỉ phương của đường thẳng đó)?

b) Giả sử tại thời điểm tính từ khi xuất phát, vật thể ở vị trí . Tính theo và .

b) Phương trình tham số của đường thẳng.

a) Vật thể chuyển động trên đường thẳng đi qua điểm và có vectơ chỉ phương là .

b) Ta có

Khi đó ta có cùng phương với Suy ra

Giải

KẾT LUẬN

Trong không gian , cho đường thẳng đi qua điểm và có vectơ chỉ phương . Hệ phương trình

được gọi là phương trình tham số của đường thẳng là tham số, .

Chú ý

• Với các số không đồng thời bằng 0, hệ phương trình xác định một đường thẳng đi qua điểm và có vectơ chỉ phương .
• Từ phương trình tham số của đường thẳng, mỗi giá trị của tham số tương ứng với một điểm thuộc đường thẳng đó và ngược lại.

Ví dụ 2. Trong không gian , cho đường thẳng

a) Hãy chỉ ra một điểm thuộc và một vectơ chỉ phương của .

b) Viết phương trình tham số của đường thẳng đi qua và có vectơ chỉ phương .

Giải

a) Do có phương trình

nên điểm thuộc và là một vectơ chỉ phương của .

b) Đường thẳng có phương trình tham số là

Trong không gian , cho đường thẳng

a) Hãy chỉ ra hai điểm thuộc và một vectơ chỉ phương của .

b) Viết phương trình tham số của đường thẳng đi qua gốc tọa độ và có vectơ chỉ phương .

Giải

a) Ta có là các điểm thuộc .

Có là một vectơ chỉ phương của . b) Phương trình tham số của đường thẳng cần tìm là:

Luyện tập 2

• HĐ3. Hình thành khái niệm phương trình chính tắc của đường thẳng

c) Phương trình chính tắc của đường thẳng

a) Điểm thuộc khi và chỉ khi hai vectơ

và cùng phương với nhau.

b) thuộc khi và chỉ khi

Giải

Vì khác 0 nên từ (1), ta có .

Vậy thuộc khi và chỉ khi

Giải

KẾT LUẬN

Trong không gian , cho đường thẳng đi qua điểm và có vectơ chỉ phương với là các số khác 0.

Hệ phương trình:

được gọi là phương trình chính tắc của đường thẳng .

Ví dụ 3. Trong không gian , cho đường thẳng .

Hãy chỉ ra một điểm thuộc và một vectơ chỉ phương của .

Giải

Đường thẳng có phương trình nên điểm thuộc và là một vectơ chỉ phương của .

Luyện tập 3

Trong không gian , cho đường thẳng . Hãy chỉ ra một vectơ chỉ phương của và hai điểm thuộc .

Giải

và thuộc và là một vectơ chỉ phương của .

Ví dụ 4. Trong không gian , viết phương trình tham số và phương trình chính tắc của đường thẳng đi qua điểm và có vectơ chỉ phương .

Giải

Đường thẳng có phương trình tham số là: và có phương trình chính tắc là: .

Trong không gian , viết phương tình tham số và phương trình chính tắc của đường thẳng đi qua điểm và có vectơ chỉ phương .

Giải

Đường thẳng đi qua điểm và có vectơ chỉ phương có

phương trình tham số là:

phương trình chính tắc là:

Luyện tập 4

Ví dụ 5. Trong không gian , viết phương trình tham số của đường thẳng đi qua điểm và vuông góc với mặt phẳng .

Mặt phẳng có vectơ pháp tuyến . Giá của và cùng vuông góc với nên chúng trùng nhau hoặc song song với nhau. Do đó nhận làm một vectơ chỉ phương.

Vậy có phương trình tham số là:

Giải

Trong không gian , viết phương trình tham số của đường thẳng đi qua điểm và vuông góc với mặt phẳng .

Giải

Ta có mặt phẳng có vectơ pháp tuyến là

Do đó nhận làm một vectơ chỉ phương.

Đường thẳng đi qua điểm và làm một vectơ chỉ phương có phương trình là: .

Luyện tập 5

• HĐ4. Lập phương trình đường thẳng đi qua hai điểm

d) Lập phương trình đường thẳng đi qua hai điểm

Giải

a) Đường thẳng  có một vectơ chỉ phương là  =

• HĐ4. Lập phương trình đường thẳng đi qua hai điểm

d) Lập phương trình đường thẳng đi qua hai điểm

Giải

b) Đường thẳng A1A2 có phương trình:.

KẾT LUẬN

Trong kông gian, cho hai điểm phân biệt và . Đường thẳng có vectơ chỉ phương

.

• Đường thẳng có phương trình tham số là: (

KẾT LUẬN

• Trong trường hợp thì đường thẳng có phương trình chính tắc là:

Ví dụ 6. Trong không gian , viết phương trình tham số và phương trình chính tắc của đường thẳng đi qua hai điểm và .

Đường thẳng đi qua và có vectơ chỉ phương . Do đó có phương trình tham số là và có phương trình chính tắc là .

Giải

Trong không gian , viết phương trình đường thẳng đi qua hai điểm và .

Luyện tập 6

Giải

Đường thắng AB đi qua điếm và có một vectơ chỉ phương có phương trình là: hay (

(H.5.27) Trong tình huống mở đầu hãy thực hiện các bước sau và trả lời câu hỏi đã được nêu ra.

Vận dụng 1

a) Viết phương trình tham số của đường thẳng .

b) Tính tọa độ giao điểm của đường thẳng với mặt phẳng .

c) Hỏi điểm có nằm giữa hai điểm và hay không?

a) Ta có

Đường thẳng MN đi qua điểm và có vectơ chỉ phương có phương trình là: , (

Giải

b) Mặt phẳng có phương trình là .

Vì D là giao điểm của đường thẳng MN với mặt phẳng Oxy nên tọa độ điểm D là nghiệm của hệ . Vậy .

Giải

c) có nên D nằm giữa M và N.

Trả lời câu hỏi trong tình huống mở đầu

Ta có nên tấm bìa che khuất tầm nhìn.

2. HAI ĐƯỜNG THẲNG VUÔNG GÓC

• HĐ5. Tìm điều kiện để hai đường thẳng vuông góc với nhau

a) Hai đường thẳng và vuông góc với nhau khi và chỉ khi hai giá của có mối quan hệ gì?

b) Tìm điều kiện đối với để và vuông góc với nhau.

a) Hai đường thẳng và vuông góc với nhau khi và chỉ khi hai giá của vuông góc với nhau.

b)

Theo câu , để và vuông góc với nhau khi và chỉ khi vuông góc với nhau.

Hay

Vậy để và vuông góc với nhau thì

Giải

KẾT LUẬN

Trong không gian , cho hai đường thẳng tương ứng có vectơ chỉ phương . Khi đó:

Ví dụ 7. Trong không gian , chứng minh rằng hai đường thẳng sau vuông góc với nhau:

Giải

Các đường thẳng tương ứng có vectơ chỉ phương , .

Do nên .

Trong không gian , cho đường thẳng . Hỏi đường thẳng có vuông góc với trục hay không?

Giải

Ta có và trục có vectơ chỉ phương là .

Có . Do đó đường thẳng không vuông góc với trục .

Luyện tập 7

Tại một nút giao thông có hai con đường. Trên thiết kế, trong không gian , hai con đường đó tương ứng thuộc hai đường thẳng:

Hỏi hai con đường trên có vuông góc với nhau hay không?

Vận dụng 2

Hai con đường thuộc hai đường thẳng lần lượt có VTCP là và

Vì nên hai con đường trên vuông góc với nhau.

Giải

3. VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG

• HĐ6. Xác định vị trí tương đối giữa hai đường thẳng

b) Giả sử và thì và có cắt nhau hay không?

c) Giả sử thi và có chéo nhau hay không?

Giải

a) . . b) Nếu thì Mà .

Suy ra và đồng phẳng. Hơn nữa nên và cắt nhau.

c)Nếu thì không vuông góc với .

Mà

Suy ra và không đồng phẳng, hay và chéo nhau.

KẾT LUẬN

Trong không gian , cho hai đường thẳng lần lượt đi qua các điểm , và tương ứng có vectơ chỉ phương . Khi đó:

• cùng phương với và .
• cùng phương với và .

KẾT LUẬN

• và cắt nhau
• và chéo nhau

Ví dụ 8. Trong không gian . Chứng mình rằng hai đường thẳng sau vuông góc với nhau và chéo nhau:

Giải

Đường thẳng đi qua điểm và có vectơ chỉ phương .

Giải

Đường thẳng đi qua điểm và có vectơ chỉ phương .

Vì nên vuông góc với .

Do đó vuông góc với .

Ta có vfa .

Do nên và chéo nhau.

Luyện tập 8

Trong không gian , chứng minh rằng hai đường thẳng sau song song với nhau:

và

Giải

Ta có đường thẳng đi qua điểm và có vectơ chỉ phương

Đường thẳng đi qua điểm và có vectơ chỉ phương .

Vì và nên .

Ví dụ 9. Trong không gian , chứng minh rằng hai đường thẳng sau cắt nhau:

Giải

Đường thẳng đi qua và có vectơ chỉ phương .

Đường thẳng đi qua và có vectơ chỉ phương . Ta có và .

Ví dụ 9. Trong không gian , chứng minh rằng hai đường thẳng sau cắt nhau:

Giải

Do và nên hai đường thẳng và cắt nhau.

Trong không gian , cho hai đường thẳng và . Chứng minh rằng:

a) Hai đường thẳng và song song với nhau

b) Đường thẳng và trục chéo nhau

c) Đường thẳng trùng với đường thẳng

d) Đường thẳng cắt trục

Luyện tập 9

Giải

Đường thẳng đi qua điểm và có vectơ chỉ phương

Đường thẳng đi qua điểm và có vectơ chỉ phương .

a) Vì và nên hai đường thẳng và song song với nhau.

Giải

b) Trục đi qua điểm và có vectơ chỉ phương là

Có và .

Có . Do đó đường thẳng và trục chéo nhau.

c) Đường thẳng  đi qua điểm và có vectơ chỉ phương

Giải

Vậy có cùng VTCP.

Lại có: B ∈ ∆3 

Nên đường thẳng ∆2 trùng với đường thẳng ∆3.

d) Trục Oz đi qua điểm O(0; 0; 0) và có vectơ chỉ phương là 

Có  và

Do đó đường thẳng ∆2 cắt trục .

Chú ý

Để xét vị tri tương đối giữa hai đường thẳng, ta cũng có thể dựa vào các vectơ chỉ phương và phương trình của hai đường thẳng đó theo tiêu chuẩn sau đây.

Trong không gian , cho hai đường thẳng tương ứng có vectơ chỉ phương và có phương trình tham số:

--------------------------------------

--------------------- Còn tiếp ----------------------