Giáo án điện tử Toán 12 kết nối Bài 16: Công thức tính góc trong không gian

CHÀO MỪNG CẢ LỚP ĐẾN VỚI TIẾT HỌC

HÔM NAY!

KHỞI ĐỘNG

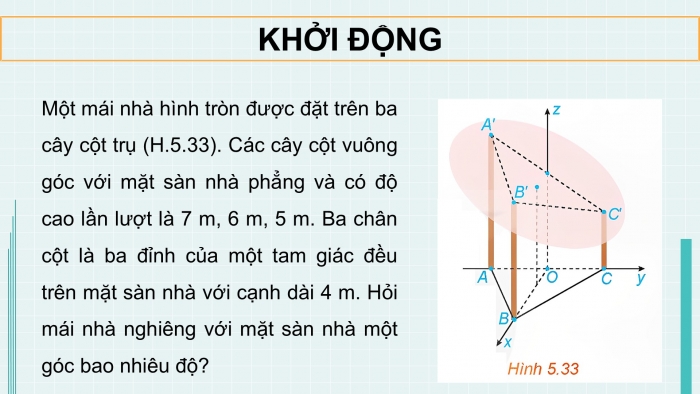
Một mái nhà hình tròn được đặt trên ba cây cột trụ (H.5.33). Các cây cột vuông góc với mặt sàn nhà phẳng và có độ cao lần lượt là 7 m, 6 m, 5 m. Ba chân cột là ba đỉnh của một tam giác đều trên mặt sàn nhà với cạnh dài 4 m. Hỏi mái nhà nghiêng với mặt sàn nhà một góc bao nhiêu độ?

CHƯƠNG V. PHƯƠNG PHÁP

TỌA ĐỘ TRONG KHÔNG GIAN

BÀI 16: CÔNG THỨC TÍNH GÓC TRONG KHÔNG GIAN

Công thức tính góc giữa hai đường thẳng

1

NỘI DUNG BÀI HỌC

Công thức tính góc giữa hai mặt phẳng

3

Công thức tính góc giữa đường thẳng và mặt phẳng

2

CÔNG THỨC TÍNH GÓC GIỮA HAI ĐƯỜNG THẲNG

1

HĐ1.

Trong không gian , cho hai đường thẳng và tương ứng có các vectơ chỉ phương (H.5.34).

a) Hãy tìm mối quan hệ giữa các góc và

b) Có nhận xét gì về mối quan hệ giữa và ?

Giải

a) Nếu thì

.

Nếu thì

.

HĐ1.

Trong không gian , cho hai đường thẳng và tương ứng có các vectơ chỉ phương (H.5.34).

a) Hãy tìm mối quan hệ giữa các góc và

b) Có nhận xét gì về mối quan hệ giữa và ?

b) Ta có:

.

Giải

KẾT LUẬN

Trong không gian , cho hai đường thẳng và tương ứng có vectơ chỉ phương ,. Khi đó:

Ví dụ 1: Trong không gian , tính góc giữa hai đường thẳng:

và

Giải

Hai đường thẳng và tương ứng có các vectơ chỉ phương , Khi đó:

Vậy .

Luyện tập 1. Trong không gian , tính góc giữa trục và đường thẳng

Giải

Đường thẳng có một vectơ chỉ phương là , trục có một vectơ chỉ phương là . Ta có:

Do đó .

CÔNG THỨC TÍNH GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG

2

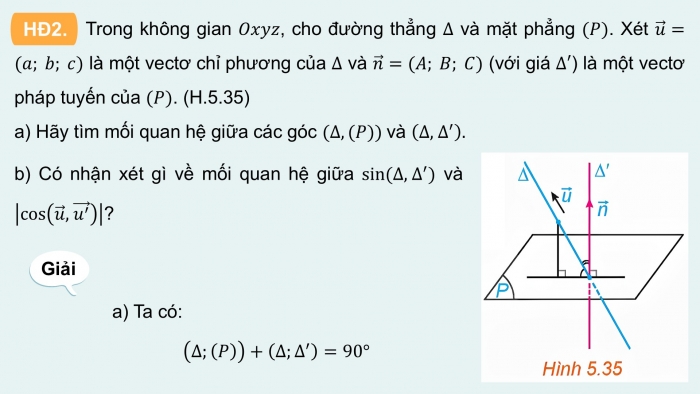
HĐ2.

Trong không gian , cho đường thẳng và mặt phẳng . Xét là một vectơ chỉ phương của và (với giá ) là một vectơ pháp tuyến của . (H.5.35)

a) Hãy tìm mối quan hệ giữa các góc và

Giải

a) Ta có:

b) Có nhận xét gì về mối quan hệ giữa và ?

HĐ2.

Trong không gian , cho đường thẳng và mặt phẳng . Xét là một vectơ chỉ phương của và (với giá ) là một vectơ pháp tuyến của . (H.5.35)

a) Hãy tìm mối quan hệ giữa các góc và

Giải

b) Ta có:

b) Có nhận xét gì về mối quan hệ giữa và ?

KẾT LUẬN

Trong không gian , cho đường thẳng có vectơ chỉ phương và mặt phẳng có vectơ pháp tuyến . Khi đó:

Ví dụ 2: Trong không gian , tính góc tạo bởi trục và mặt phẳng :

Giải

Trục có vectơ chỉ phương , mặt phẳng có vectơ pháp tuyến Ta có:

Vậy tạo với góc .

Luyện tập 2. Trong không gian , tính góc giữa đường thẳng và

Giải

Đường thẳng có một vectơ chỉ phương là , mặt phẳng có một vectơ pháp tuyến . Ta có:

.

CÔNG THỨC TÍNH GÓC

GIỮA HAI MẶT PHẲNG

3

HĐ3.

Trong không gian , cho hai mặt phẳng tương ứng có các vectơ pháp tuyến là , Lấy các đường thẳng tương ứng có vectơ chỉ phương . (H.5.36)

a) Góc giữa hai mặt phẳng và và góc giữa hai đường thẳng và có mối quan hệ gì?

b) Tính côsin của góc giữa hai mặt phẳng và .

Giải

a) .

HĐ3.

Trong không gian , cho hai mặt phẳng tương ứng có các vectơ pháp tuyến là , Lấy các đường thẳng tương ứng có vectơ chỉ phương . (H.5.36)

a) Góc giữa hai mặt phẳng và và góc giữa hai đường thẳng và có mối quan hệ gì?

b) Tính côsin của góc giữa hai mặt phẳng và .

Giải

b)

KẾT LUẬN

Trong không gian , cho hai mặt phẳng tương ứng có các vectơ pháp tuyến là , . Khi đó, góc giữa và , kí hiệu là , được tính theo công thức:

Ví dụ 3: Trong không gian , tính góc giữa hai mặt phẳng

và

Giải

Các mặt phẳng tương ứng có các vectơ pháp tuyến là , Ta có:

Do đó .

Luyện tập 3. Trong không gian , tính góc giữa hai mặt phẳng và

Giải

Mặt phẳng có một vectơ pháp tuyến là , mặt phẳng có một vectơ pháp tuyến là . Ta có:

Ví dụ 4: Trong không gian , cho , , , Tính góc giữa hai mặt phẳng và

Giải

Mặt phẳng có cặp vectơ chỉ phương là và

Suy ra có vectơ pháp tuyến

Do đó cũng là vectơ pháp tuyến của

Mặt phẳng có cặp vectơ chỉ phương là và

Suy ra có vectơ pháp tuyến là .

Do đó cũng là vectơ pháp tuyến của

Giải

Gọi là góc giữa hai mặt phẳng và Khi đó:

Vậy

Vận dụng. Hãy trả lời câu hỏi đã được nêu ra trong tình huống mở đầu.

Giải

Giả sử , tam giác đều cạnh bằng nên .

Đơn vị trên các trục tọa độ là mét, nên ta có:

.

, .

Một vectơ pháp tuyến của mặt phẳng là:

.

Vận dụng. Hãy trả lời câu hỏi đã được nêu ra trong tình huống mở đầu.

Mặt phẳng tọa độ có một vectơ pháp tuyến là . Khi đó:

.

Vậy góc giữa mái nhà và mặt sàn gần bằng .

Giải

HOẠT ĐỘNG

LUYỆN TẬP

TRÒ CHƠI “Bắn cung”

Chia hai đội chơi, mỗi đội 2 thành viên. Sẽ có 5 câu hỏi, mỗi câu hỏi có 30 giây suy nghĩ và trả lời. Hết 30 giây đội nào có câu trả lời nhanh và đúng nhất sẽ được quyền bắn tên. Kết thúc trò chơi đội nào bắn được nhiều tên hơn sẽ thắng.

KHỞI ĐỘNG

ĐỘI 1

ĐỘI 2

Câu 1: Tính số đo góc giữa mặt phẳng và mặt phẳng .

A. .

C.

Câu 2: Trong không gian , cho hai mặt phẳng và . Biết rằng điểm là hình chiếu vuông góc của gốc tọa độ xuống mặt phẳng . Số đo góc giữa hai mặt phẳng và mặt phẳng bằng :