Giáo án điện tử Toán 12 chân trời Bài 2: Tích phân

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC!

Một ô tô đang di chuyển với vận tốc thì hãm phanh nên tốc độ của xe thay đổi theo thời gian (giây) được tính theo công thức

Kể từ khi hãm phanh đến khi dừng, ô tô đi được quãng đường bao nhiêu?

KHỞI ĐỘNG

CHƯƠNG IV:

NGUYÊN HÀM. TÍCH PHÂN

BÀI 2: TÍCH PHÂN

1

Diện tích hình thang cong

Khái niệm tích phân

Tính chất của tích phân

NỘI DUNG BÀI HỌC

DIỆN TÍCH HÌNH THANG CONG

HĐKP1

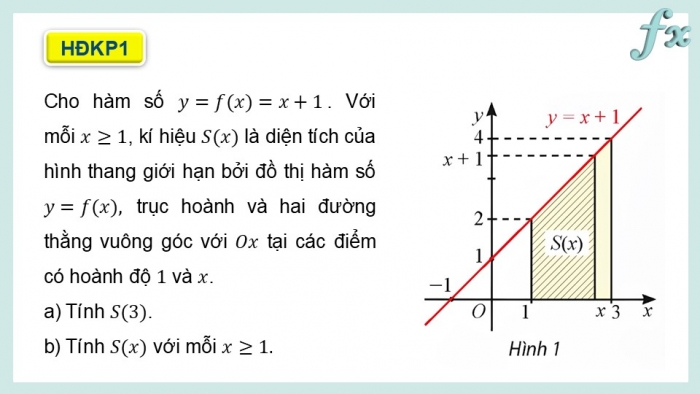
Cho hàm số . Với mỗi , kí hiệu là diện tích của hình thang giới hạn bởi đồ thị hàm số trục hoành và hai đường thằng vuông góc với tại các điểm có hoành độ và .

a) Tính .

b) Tính với mỗi

HĐKP1

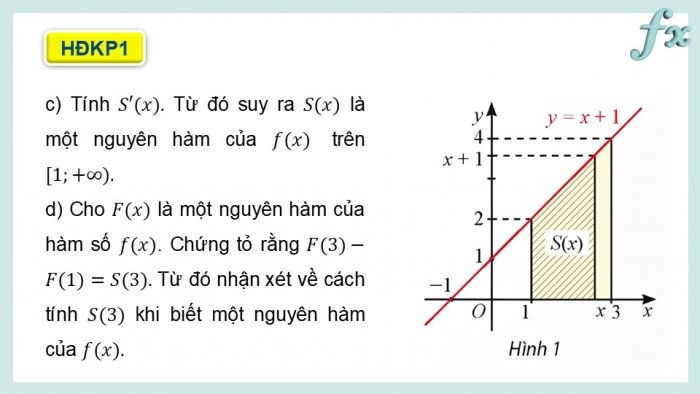
c) Tính Từ đó suy ra là một nguyên hàm của trên

d) Cho là một nguyên hàm của hàm số . Chứng tỏ rằng Từ đó nhận xét về cách tính khi biết một nguyên hàm của

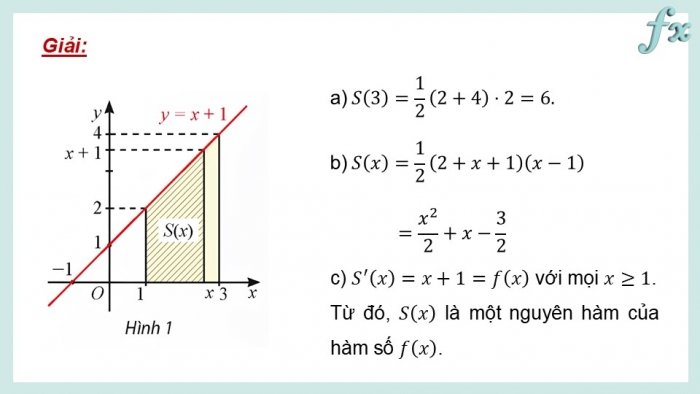
Giải:

c) với mọi .

Từ đó, là một nguyên hàm của hàm số .

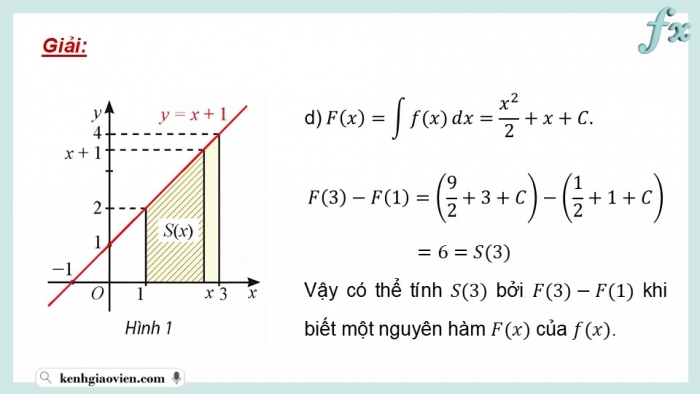
Giải:

Vậy có thể tính bởi khi biết một nguyên hàm của .

Kết luận

Cho hàm số liên tục và không âm trên đoạn . Hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng được gọi là hình thang cong.

- Nếu hàm số liên tục và không âm trên đoạn thì diện tích của hình thang cong giới hạn bởi đồ thị hàm số , trục

hoành và hai đường thẳng được tính bởi trong đó là một nguyên hàm của trên đoạn .

Hàm số liên tục, dương trên đoạn và có một nguyên hàm là

Do đó, diện tích hình thang cong cần tìm là

Ví dụ 1: Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng (Hình 3).

Giải:

Thực hành 1

Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số trục hoành, trục tung và đường thẳng (Hình 4).

Giải:

Ta có hàm số liên tục, nhận giá trị dương trên và có một nguyên hàm là .

Do đó, diện tích hình thang cong cần tìm là

.

KHÁI NIỆM TÍCH PHÂN

kenhgiaovien

/

• Bài giảng và giáo án này chỉ có duy nhất trên kenhgiaovien.com
• Bất cứ nơi nào đăng bán lại đều là đánh cắp bản quyền và hưởng lợi bất chính trên công sức của giáo viên.
• Vui lòng không tiếp tay cho hành vi xấu.

Zalo: 0386 168 725

HĐKP2

Cho hàm số . Lấy hai nguyên hàm tuỳ ý và của rồi tính và Nhận xét về kết quả nhận được.

Giải:

Chẳng hạn lấy và .

Ta có

.

Vậy .

Kết luận

Cho hàm số liên tục trên đoạn . Nếu là một nguyên hàm của trên đoạn thì hiệu số được gọi là tích phân từ đến của hàm số , kí hiệu .

Kết luận

Cho hàm số liên tục trên đoạn . Nếu là một nguyên hàm của trên đoạn thì hiệu số được gọi là tích phân từ đến của hàm số , kí hiệu .

Ta gọi là dấu tích phân, và là cận tích phân, là cận dưới, là cận trên, là biểu thức dưới dấu tích phân và là hàm số dưới dấu tích phân.

Chú ý:

a) Trong trường hợp hoặc , ta quy ước

b) Người ta chứng minh được rằng, tích phân chỉ phụ thuộc vào hàm số và các cận mà không phụ thuộc vào biến số hay ,

Chú ý:

c) Ý nghĩa hình học của tích phân

Nếu hàm số liên tục và không âm trên đoạn thì là diện tích của hình thang cong giới hạn bởi

đồ thị hàm số , trục hoành và hai đường thẳng , .

Ví dụ 2: Tính các tích phân sau:

Giải:

Chú ý:

a) Nếu hàm số có đạo hàm và liên tục trên đoạn thì .

b) Ta đã biết rằng, đạo hàm của quãng đường di chuyển của vật theo thời gian bằng tốc độ của chuyển động tại mỗi thời điểm . Do đó, nếu biết tốc độ tại mọi thời điểm thì tính được quãng đường di chuyển trong khoảng thời gian từ đến theo công thức .

Ví dụ 3: Xét tình huống ở hoạt động Khởi động (trang 12)

a) Tính quãng đường xe di chuyển từ khi hãm phanh đến khi dừng.

b) Tính tốc độ trung bình của xe trong khoảng thời gian đó.

Giải:

a) Xe dừng khi hay với mọi

Từ đó, quãng đường xe di chuyển từ khi bắt đầu hãm phanh đến khi dừng là

b) Tốc độ trung bình của xe trong khoảng thời gian đó là:

Nhận xét: Cho hàm số liên tục trên đoạn . Khi đó được gọi là giá trị trung bình của hàm số trên đoạn .

Ví dụ 3: Xét tình huống ở hoạt động Khởi động (trang 12)

a) Tính quãng đường xe di chuyển từ khi hãm phanh đến khi dừng.

b) Tính tốc độ trung bình của xe trong khoảng thời gian đó.

Giải:

Thực hành 2

Tính các tích phân sau:

Vận dụng 1

Sau khi xuất phát, ô tô di chuyển với tốc độ

trong đó tính theo m/s, thời gian tính theo giây với là thời điểm xe xuất phát.

a) Tính quãng đường xe đi được sau giây, sau giây.

b) Tính tốc độ trung bình của xe trong khoảng thời gian từ đến .

Giải:

a) Quãng đường xe đi được sau giây là

Với thì .

Với thì .

b) Tốc độ trung bình của xe trong khoảng thời gian từ đến là:

TÍNH CHẤT CỦA TÍCH PHÂN

a) Tìm một nguyên hàm của hàm số . Từ đó,

c) Có nhận xét gì về giá trị của và ?

Giải:

Tính chất 1

HĐKP3

a) Tìm một nguyên hàm của hàm số . Từ đó,

c) Có nhận xét gì về giá trị của và ?

Giải:

Tính chất 1

c) .

HĐKP3

Kết luận

Cho hàm số liên tục trên đoạn là số thực.

Khi đó:

Ví dụ 4: Tính các tích phân sau:

Giải:

Giải:

Thực hành 3

Tính các tích phân sau:

a) Tìm một nguyên hàm của hàm số . Từ

c) Có nhận xét gì về hai kết quả trên?

Tính chất 2

HĐKP4

Giải:

Kết luận

Cho hai hàm số liên tục trên đoạn . Khi đó:

Ví dụ 5: Tính các tích phân sau:

Ví dụ 6: Tại một nhà máy, gọi là tổng chi phí (tính theo triệu đồng) để sản xuất tấn sản phẩm A trong một tháng. Khi đó, đạo hàm gọi là chi phí cận biên, cho biết tốc độ tăng tổng chi phí theo lượng sản phẩm được sản xuất. Giả sử chi phí cận biên (tính theo triệu đồng trên tấn) của nhà máy được ước lượng bởi công thức

với

Biết rằng triệu đồng, gọi là chi phí cố định. Tính tổng chi phí khi nhà máy sản xuất tấn sản phẩm A trong tháng.

Giải:

Ta có:

Suy ra (triệu đồng).

Vậy khi nhà máy sản xuất tấn sản phẩm A trong tháng thì tổng chi phí là triệu đồng.

Thực hành 4

Tính các tích phân sau:

Giải:

Thực hành 4

Tính các tích phân sau:

Giải:

Thực hành 4

Tính các tích phân sau:

Giải:

Tại một nhà máy sản xuất một loại phân bón, gọi là lợi nhuận (tính theo triệu đồng) thu được từ việc bán tấn sản phẩm trong một tuần. Khi đó, đạo hàm gọi là lợi nhuận cận biên, cho biết tốc độ tăng lợi nhuận theo lượng sản phẩm bán được. Giả sử lợi nhuận cận biên (tính theo triệu đồng trên tấn) của nhà máy được ước lượng bởi công thức

với .

Tính lợi nhuận nhà máy thu được khi bán tấn sản phẩm trong tuần. Biết rằng nhà máy lỗ triệu đồng nếu không bán được lượng sản phẩm nào trong tuần.

Vận dụng 2

Giải:

Theo giả thiết,

Vậy nếu trong tuần nhà máy bán được tấn sản phẩm thì thu được lợi nhuận là đồng.

--------------------------------------

--------------------- Còn tiếp ----------------------