Giáo án và PPT Toán 11 cánh diều Bài tập cuối chương II

CHƯƠNG II. DÃY SỐ. CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN

BÀI TẬP CUỐI CHƯƠNG II

HOẠT ĐỘNG KHỞI ĐỘNG

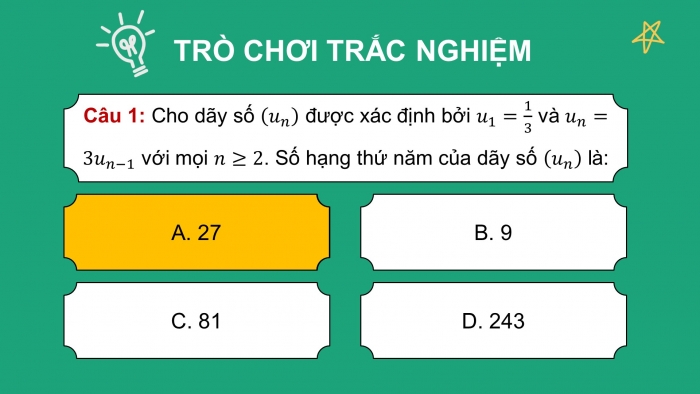
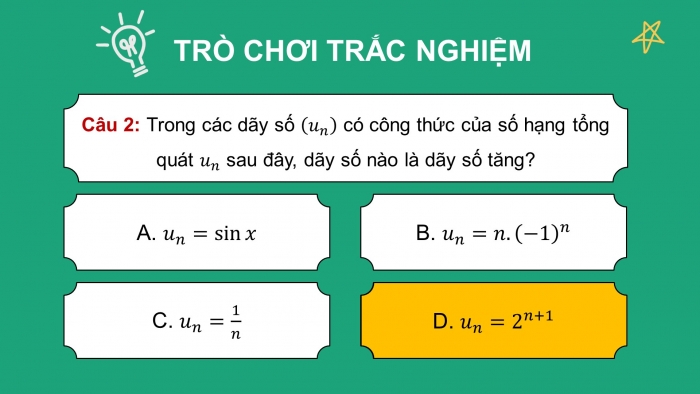
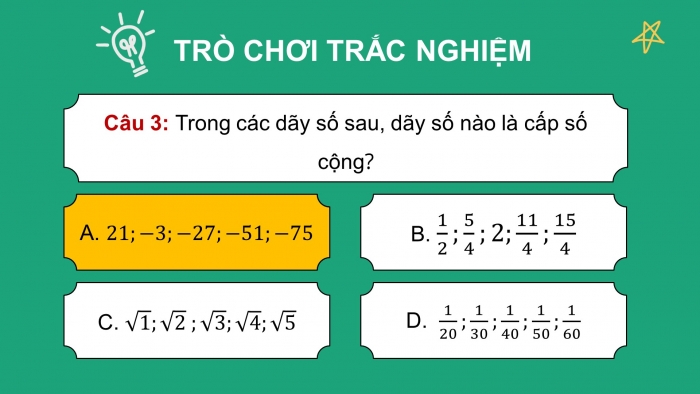
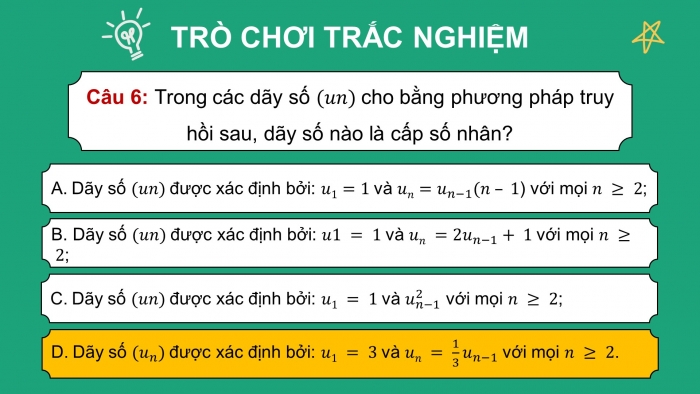
-  GV trình chiếu câu hỏi củng cố, cho HS suy nghĩ và trả lời.

Trả lời nhanh các câu hỏi trắc nghiệm trong SGK – tr.57 (từ câu 1 đến câu 7) và yêu cầu HS giải thích tại sao lại chọn được đáp án đó.

- GV gọi đại diện một số thành viên nhóm HS trả lời, HS khác nhận xét, bổ sung, dẫn dắt vào bài học mới.

HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC

- GV yêu cầu HS nhắc lại kiến thức đã học:

Nhóm 1: Thực hiện hệ thống hóa kiến thức bài Dãy số.         

• Khái niệm dãy số hữu hạn?
• Khái niệm dãy số vô hạn?
• Cách cho một dãy số?
• Khái niệm dãy số tăng, dãy số giảm
• Thế nào là dãy số bị chặn trên?
• Thế nào là dãy số bị chặn dưới?
• Thế nào là dãy số bị chặn?

Nhóm 2: Thực hiện hệ thống hóa kiến thức bài Cấp số cộng.

• Định nghĩa cấp số cộng?
• Số hạng tổng quát của một cấp số cộng?
• Tổng n số hạng đầu của cấp số cộng?

Nhóm 3: Thực hiện hệ thống hóa kiến thức bài Cấp số nhân.

• Định nghĩa của cấp số nhân?
• Số hạng tổng quát cảu cấp số nhân? 
• Tổng n số hạng đầu của một cấp số nhân?

Sản phẩm dự kiến:

Ôn tập kiến thức đã học trong chương II

* Nhóm 1:

+ Mỗi hàm số được gọi là một dãy số hữu hạn.

Do mỗi số nguyên dương k tương ứng với đúng một số nên ta có thể viết dãy số đó dưới dạng khai triển: .

+ Số được gọi là số hạng đầu, số được gọi là số hạng cuối của dãy số đó.

+ Mỗi hàm số: được gọi là một dãy số vô hạn.

Do mỗi số nguyên dương n tương ứng với đúng một số nên ta có thể viết dãy số đó dưới dạng khai triển:

+ Dãy số đó còn được viết tắt là .

- Liệt kê các số hạng của dãy số đó (với những dãy số hữu hạn và có ít số hạng).

- Diễn đạt bằng lời cách xác định mỗi số hạng của dãy số đó.

- Cho công thức của số hạng tổng quát của dãy số đó.

- Cho bằng phương pháp truy hồi.

+ Dãy số được gọi là dãy số tăng nếu với mọi .

+ Dãy số được gọi là dãy số giảm nếu với mọi .

- Dãy số được gọi là bị chặn trên nếu tồn tại một số M sao cho với mọi .

- Dãy số được gọi là bị chặn dưới nếu tồn tại một số m sao cho với mọi .

- Dãy số được gọi là bị chặn nếu nó vừa bị chặn trên, vừa bị chặn dưới; tức là tồn tại các số m và M sao cho với mọi .

* Nhóm 2:

Cấp số cộng là một dãy số, trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng tổng của số hạng đứng ngay trước nó với một số không đổi d, tức là:

với

Số d được gọi là công sai của cấp số cộng.

Nếu cấp số cộng có số hạng đầu và công sai d thì số hạng tổng quát được xác định bởi công thức:

với .

Cho cấp số cộng có số hạng đầu và công sai d. Đặt .

Khi đó:

Nhóm 3:

Cấp số nhân là một dãy số, trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng tích của số hạng đứng ngay trước nó với một số không đổi q, tức là:

với

Số q được gọi là công bội của cấp số nhân.

Nếu cấp số nhân có số hạng đầu và công bội q thì số hngj tổng quát được xác định bởi công thức:

với

Cho cấp số nhân có số hạng đầu và công bội .

Đặt . Khi đó:

HOẠT ĐỘNG LUYỆN TẬP

Yêu cầu: HS vận dụng các kiến thức của bài học hoàn thành bài tập thông qua đưa ra câu trả lời đúng cho các câu hỏi trắc nghiệm.

Câu 1. Cho cấp số cộng có tổng n số hạng đầu là  Sn = 3n² + 4n, n ∈ N*. Giá trị của số hạng thứ 10 của cấp số cộng là

A. u₁₀=55

B. u₁₀=67

C. u₁₀=61

D. u₁₀=59

Câu 2. Một khu rừng có trữ lượng gỗ là 4.10⁵ mét khối. Biết tốc độ sinh trưởng của các cây ở khu rừng đó là 4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ?

A. 4.10⁵.(0,05)⁵

B. 4.(10,4)⁵

C. 4.10⁵.(1,04)⁴

D. 4.10⁵.(1,4)⁵

Câu 3. Tổng 1+2+22+...+2²⁰¹⁷ có giá trị bằng

A. 2²⁰¹⁸

B. 2²⁰¹⁷

C. 2²⁰¹⁸⁻¹

D. 2²⁰¹⁷⁻¹

Câu 4. Gọi S là tập hợp tất cả các giá trị của tham số m để phương trình x⁴ – (9m+1)x² + m = 0 có 4 nghiệm phân biệt lập thành cấp số cộng. Tổng giá trị của các phần tử thuộc S là

A. 9/19

B. 2/89

C. 1/39

D. 8/29

Câu 5. Một tứ giác lồi có số đo các góc lập thành một cấp số nhân. Biết rằng số đo của góc nhỏ nhất bằng 1/9 số đo của góc nhỏ thứ ba. Số đo của các góc trong tứ giác đó lần lượt là

A. 5°; 15°; 45°; 225°.

B.  9°; 27°; 81°; 243°.

C.  7°; 21°; 63°; 269°.

D.  8°; 32°; 72°; 248°.

Sản phẩm dự kiến:

HOẠT ĐỘNG VẬN DỤNG

GV yêu cầu HS thảo luận cặp đôi, hoàn thành hai bài tập sau:

Bài 1. Cho cấp số cộng (u_n) có u₁ = −2 và công sai d = 3. Hỏi có bao nhiêu số hạng thỏa mãn điều kiện u_n < 11.

Bài 2. Tìm tất cả các giá trị của tham số m để phương trình sau có ba nghiệm phân biệt lập thành một cấp số nhân: x³ - 7x² + 2(m² + 6m)x - 8 = 0.

Sản phẩm dự kiến:

Bài 1: Cấp số cộng có u₁ = −2 và công sai d = 3 nên số hạng tổng quát của cấp số cộng là:

u_n = u₁ + (n − 1) . d = −2 + 3(n − 1) = 3n − 5

Để u_n < 11 thì 3n − 5 < 11

Mà n nguyên dương nên n ∈ { 1,2,3,4,5}

Vậy có 5 số hạng của cấp số cộng thỏa mãn điều kiện

Bài 2.

+ Điều kiện cần:

Giả sử phương trình đã cho có ba nghiệm phân biệt x₁, x₂, x₃, lập thành một cấp số nhân.

Theo định lý Vi-ét, ta có x₁.x₂.x₃= 8 

Theo tính chất của cấp số nhân, ta có x₁.x₃=8

Suy ra x = 2. 

Với nghiệm x = 2 

Ta có m² +6m-7=0 => [m = 1, m = - 7

+ Điều kiện đủ: Với m = 1 hoặc m = - 7 thì m² + 6m = 7 

Nên ta có phương trình x³- 7x² + 14x - 8 = 0 Giải phương trình này, ta được các nghiệm là 1,2,4.

Hiển nhiên ba nghiệm này lập thành một cấp số nhân Với công bội q = 2

Vậy m = 1 và m = - 7 là các giá trị cần tìm.m=1

Vậy m=1 thì ba đường thẳng đã cho đồng quy tại 1 điểm.