Giáo án và PPT Toán 11 cánh diều Bài 1: Giới hạn của dãy số
Đồng bộ giáo án word và powerpoint (ppt) Bài 1: Giới hạn của dãy số. Thuộc chương trình Toán 11 cánh diều. Giáo án được biên soạn chỉn chu, hấp dẫn. Nhằm tạo sự lôi cuốn và hứng thú học tập cho học sinh.
Click vào ảnh dưới đây để xem giáo án WORD rõ nét












Giáo án ppt đồng bộ với word









Còn nữa....
Các tài liệu bổ trợ khác
Xem toàn bộ: Trọn bộ giáo án và PPT Toán 11 cánh diều
CHƯƠNG III. GIỚI HẠN. HÀM SỐ LIÊN TỤC
BÀI 1. GIỚI HẠN DÃY SỐ
HOẠT ĐỘNG KHỞI ĐỘNG
GV yêu cầu HS thảo luận và trả lời:
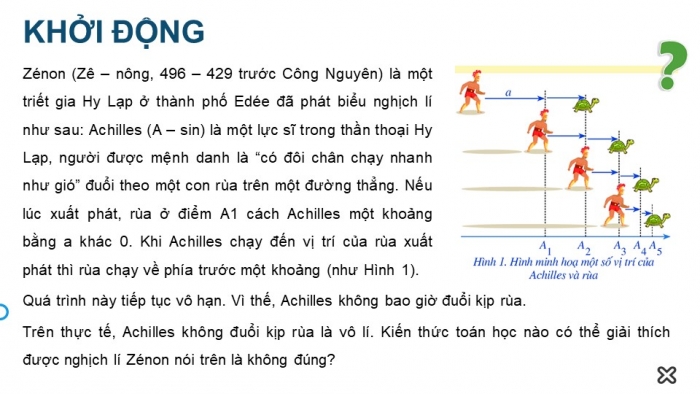
Zénon (Zê – nông, 496 – 429 trước Công Nguyên) là một triết gia Hy Lạp ở thành phố Edée đã phát biểu nghịch lí như sau: Achilles (A – sin) là một lực sĩ trong thần thoại Hy Lạp, người được mệnh danh là “có đôi chân chạy nhanh như gió” đuổi theo một con rùa trên một đường thẳng. Nếu lúc xuất phát, rùa ở điểm A1 cách Achilles một khoảng bằng a khác 0. Khi Achilles chạy đến vị trí của rùa xuất phát thì rùa chạy về phía trước một khoảng (như Hình 1). Quá trình này tiếp tục vô hạn. Vì thế, Achilles không bao giờ đuổi kịp rùa.
Trên thực tế, Achilles không đuổi kịp rùa là vô lí. Kiến thức toán học nào có thể giải thích được nghịch lí Zénon nói trên là không đúng?
HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC
1. GIỚI HẠN HỮU HẠN CỦA DÃY SỐ
Hoạt động 1: Định nghĩa
HS thảo luận trả lời câu hỏi:
- Thực hiện HĐ1.
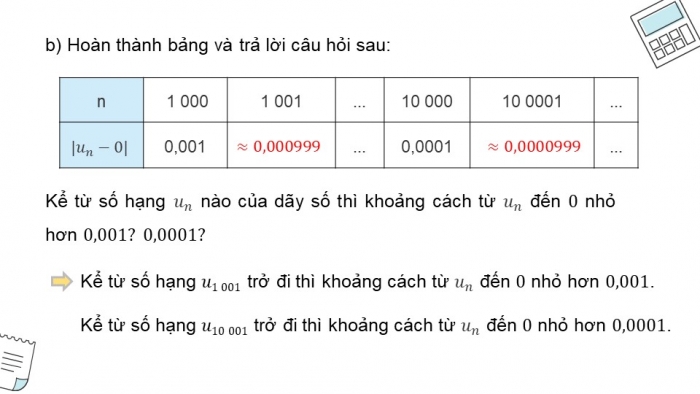
- Dãy số
 có giới hạn 0 khi n tiến tới dương vô cực khi nào?
có giới hạn 0 khi n tiến tới dương vô cực khi nào? - Khi nào thì
 ?
? - Hoàn thành luyện tập 1.
- Thực hiện HĐ2.
- Dãy số
 có giới hạn hữu hạn là a khi n tiến tới dương vô cực khi nào?
có giới hạn hữu hạn là a khi n tiến tới dương vô cực khi nào? - Hoàn thành luyện tập 2.
Sản phẩm dự kiến:
HĐ 1:
a) Khi n ngày càng lớn thì giá trị của ![]() càng giảm dần về 0.
càng giảm dần về 0.
b) Ta có bảng:
(Bảng dưới)
Định nghĩa
Dãy số ![]() có giới hạn 0 khi
có giới hạn 0 khi ![]() dần tới dương vô cực, nếu
dần tới dương vô cực, nếu ![]() nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi, kí hiệu
nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi, kí hiệu ![]() hay
hay ![]() khi
khi ![]() . Ta còn viết là
. Ta còn viết là ![]() .
.
Nhận xét:
Nếu ![]() ngày càng gần tới 0 khi n ngày càng lớn thì
ngày càng gần tới 0 khi n ngày càng lớn thì ![]()
Ví dụ 1 (SGK -tr.60)
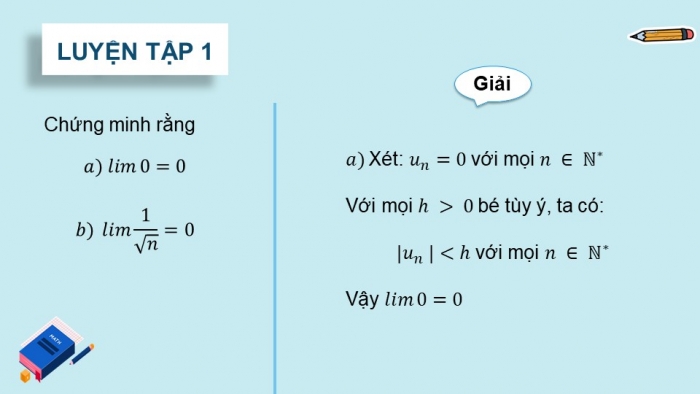
Luyện tập 1
a) Xét: ![]() với mọi
với mọi ![]()
Với mọi h > 0 bé tùy ý, ta có:
![]() với mọi
với mọi ![]()
Vậy lim 0 = 0.
b) Xét: ![]() với mọi
với mọi ![]()
Với mọi ![]() bé tùy ý, ta có
bé tùy ý, ta có
![]()
Vậy với các số tự nhiên n lớn hơn ![]() thì
thì ![]()
Theo định nghĩa, ta có ![]() .
.
HĐ 2:
Ta có ![]()
Định nghĩa
Dãy số ![]() có giới hạn hữu hạn là
có giới hạn hữu hạn là ![]() khi
khi ![]() dần tới dương vô cực, nếu lim
dần tới dương vô cực, nếu lim ![]() . Khi đó, ta viết
. Khi đó, ta viết ![]() hay
hay ![]() hay
hay ![]() khi
khi ![]() .
.
Ví dụ 2 (SGK -tr.61)
Chú ý:
+ Một dãy số có giới hạn thì giới hạn đó là duy nhất
+ Không phải dãy số nào cũng có giới hạn, chẳng hạn như dãy số ![]() với
với ![]() .
.
Luyện tập 2
Đặt ![]()
Do ![]()
Vậy ![]()
Hoạt động 2: Một số giới hạn cơ bản
HS thảo luận trả lời câu hỏi:
- Nêu một số giới hạn cơ bản.
- Hoàn thành luyện tập 3.
Sản phẩm dự kiến:
Ta thừa nhận các giới hạn sau
a) ![]() với k là số nguyên dương cho trước;
với k là số nguyên dương cho trước;
b) ![]() với c là hằng số, k là số nguyên dương cho trước.
với c là hằng số, k là số nguyên dương cho trước.
c) Nếu ![]() thì
thì ![]()
d) Dãy số ![]() với
với ![]() có giới hạn là một số vô tỉ và gọi giới hạn đó là e.
có giới hạn là một số vô tỉ và gọi giới hạn đó là e.
![]()
Một giá trị gần đúng của e là 2,718281828459045.
Ví dụ 3 (SGK -tr.62)
Luyện tập 3
Ta có 0< ![]() do đó
do đó ![]()
2. ĐỊNH LÍ VỀ GIỚI HẠN HỮU HẠN
HS thảo luận trả lời câu hỏi:
- Thực hiện HĐ3.
- Nêu định lí về giới hạn hữu hạn của một tổng, của một hiệu, của một tích, của một thường và của một số căn thức.
- Hoàn thành luyện tập 4.
Sản phẩm dự kiến:
HĐ 3.

Suy ra
Vậy ![]()
c) Ta có:
![]()
![]()
![]()
Suy ra ![]()
Ta có:
![]()
Vậy ![]()
Kết luận
a) Nếu ![]() thì:
thì:
b) Nếu ![]() và
và ![]() thì
thì
![]() và
và ![]() .
.
Ví dụ 4 (SGK -tr.62)
Luyện tập 4 (SGK -tr.63)
a) ![]()
b) 
3. TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN
HS thảo luận trả lời câu hỏi:
- Thực hiện HĐ4.
- Thế nào là cấp số nhân lùi vô hạn.
- Công thức tính tổng của cấp số nhân lùi vô hạn đã cho?
- Hoàn thành luyện tập 5 và luyện tập 6.
Sản phẩm dự kiến:
HĐ 4:
a) Ta có ![]()
b) 
 Kết luận
Kết luận
Cấp số nhân vô hạn ![]() có công bội
có công bội ![]() thỏa mãn
thỏa mãn ![]() được gọi là cấp số nhân lùi vô hạn.
được gọi là cấp số nhân lùi vô hạn.
Tổng của cấp số nhân lùi vô hạn đã cho là:
![]()
Ví dụ 5 (SGK -tr.63)
Ví dụ 6 (SGK -tr.63)
Luyện tập 5
Ta có dãy số ![]() là một cấp số nhân lùi vô hạn với số hạng đầu
là một cấp số nhân lùi vô hạn với số hạng đầu ![]() và công bội
và công bội ![]()
Nên ![]()
Luyện tập 6
Thời gian Achilles chạy hết các quãng đường có độ dài 100 km, 1 km, ![]() km,
km, ![]() km,... lần lượt là 1h,
km,... lần lượt là 1h, ![]() ,
, ![]()
Vậy thời gian đi hết quãng đường trên là
![]()
Ta có ![]()
Vậy Archilles đuổi kịp rùa sau ![]() giờ.
giờ.
4. GIỚI HẠN VÔ CỰC
HS thảo luận trả lời câu hỏi:
- Thực hiện HĐ5.
- Khi nào ta nói nói dãy số (un) có giới hạn là +∞?
- Khi nào ta nói nói dãy số (un) có giới hạn là -∞?
- Hoàn thành luyện tập 7 và luyện tập 8.
Sản phẩm dự kiến:
HĐ 5:
Ta có: khi ![]() thì
thì ![]()
Khi đó ![]() có thể lớn tùy ý kể từ một số hạng nào đó trở đi.
có thể lớn tùy ý kể từ một số hạng nào đó trở đi.
Kết luận
- Ta nói dãy số ![]() có giới hạn là
có giới hạn là ![]() khi
khi ![]() nếu
nếu ![]() lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Kí hiệu ![]() hay
hay ![]() khi
khi ![]() .
.
- Ta nói dãy số ![]() có giói hạn là
có giói hạn là ![]() khi
khi ![]() nếu
nếu ![]()
Kí hiệu ![]() hay
hay ![]() khi
khi ![]() .
.
Ví dụ 7 (SGK -tr.64)Luyện tập 7
Xét dãy số ![]()
Với M là số dương bất kì, ta thấy ![]()
Vậy với các số tự nhiên ![]() thì
thì ![]() .
.
Do đó, ![]()
Nhận xét:
+) ![]() (với k là số nguyên dương cho trước).
(với k là số nguyên dương cho trước).
+) ![]() (với
(với ![]() là số thực cho trước.
là số thực cho trước.
+) Nếu ![]() và
và ![]() thì
thì ![]()
+) Nếu ![]() và
và ![]() với mọi n thì
với mọi n thì ![]()
+) ![]()
Ví dụ 8 (SGK -tr.64)
Luyện tập 8
![]()
HOẠT ĐỘNG LUYỆN TẬP
Câu 1: Giá trị lim (n3−2n+1) bằng:
A. 0
B. 1
C. −∞
D. +∞
Câu 2: Cho (un) là một cấp số nhân công bội q=1/3 và số hạng đầu u1=2. Đặt S = u1 + u2 + …+ un. Khi đó limSn bằng
A. 1
B. 2/3
C. 4/3
D. 3
Câu 3: Giá trị lim(5n – n2 + 1) bằng:
A. 0
B. 1
C. −∞
D. +∞
Sản phẩm dự kiến:
Câu 1: B
Câu 2: A
Câu 3: B
HOẠT ĐỘNG VẬN DỤNG
Vận dụng kiến thức, GV yêu cầu HS trả lời câu hỏi:
Câu 1: Tính các giới hạn sau:
a) ![]()
b) ![]()
Câu 2: Tính các giới hạn sau:
a) ![]()
b) ![]()
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Hệ thống có đầy đủ các tài liệu:
- Giáo án word (300k)
- Giáo án Powerpoint (350k)
- Trắc nghiệm theo cấu trúc mới (150k)
- Đề thi cấu trúc mới: ma trận, đáp án, thang điểm..(150k)
- Phiếu trắc nghiệm câu trả lời ngắn (150k)
- Trắc nghiệm đúng sai (150k)
- Lý thuyết bài học và kiến thức trọng tâm (150k)
- File word giải bài tập sgk (150k)
- Phiếu bài tập để học sinh luyện kiến thức (150k)
- ....
=> Có thể chọn nâng cấp VIP với phí là 1050k để tải tất cả tài liệu trên.
- Gửi trước 500k. Tải về dùng thực tế. 1 ngày sau mới gửi phí còn lại
Cách tải hoặc nâng cấp:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB(QR)
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Trọn bộ giáo án và PPT Toán 11 cánh diều
TÀI LIỆU GIẢNG DẠY TOÁN 11 KẾT NỐI TRI THỨC
Giáo án toán 11 kết nối tri thức đủ cả năm
Giáo án điện tử toán 11 kết nối tri thức
Giáo án chuyên đề Toán 11 kết nối tri thức đủ cả năm
Giáo án điện tử chuyên đề toán 11 kết nối tri thức
Giáo án dạy thêm toán 11 kết nối tri thức đủ cả năm
Giáo án powerpoint dạy thêm toán 11 kết nối tri thức đủ cả năm
Trò chơi khởi động Toán 11 kết nối tri thức
Câu hỏi và bài tập trắc nghiệm toán 11 kết nối tri thức
Đề thi toán 11 kết nối tri thức
File word đáp án toán 11 kết nối tri thức
Bài tập file word Toán 11 kết nối tri thức
Kiến thức trọng tâm Toán 11 kết nối tri thức
Đề kiểm tra 15 phút Toán 11 kết nối tri thức
Phiếu học tập theo bài Toán 11 kết nối tri thức cả năm
Trắc nghiệm đúng sai Toán 11 kết nối tri thức cả năm
Trắc nghiệm dạng câu trả lời ngắn Toán 11 kết nối tri thức cả năm
TÀI LIỆU GIẢNG DẠY TOÁN 11 CHÂN TRỜI SÁNG TẠO
Giáo án toán 11 chân trời sáng tạo đủ cả năm
Giáo án điện tử toán 11 chân trời sáng tạo
Giáo án chuyên đề Toán 11 chân trời sáng tạo đủ cả năm
Giáo án điện tử chuyên đề Toán 11 chân trời sáng tạo
Giáo án dạy thêm toán 11 chân trời sáng tạo đủ cả năm
Giáo án powerpoint dạy thêm toán 11 chân trời sáng tạo đủ cả năm
Trò chơi khởi động Toán 11 chân trời sáng tạo
Câu hỏi và bài tập trắc nghiệm toán 11 chân trời sáng tạo
Đề thi toán 11 chân trời sáng tạo
File word đáp án toán 11 chân trời sáng tạo
Bài tập file word toán 11 chân trời sáng tạo
Kiến thức trọng tâm Toán 11 chân trời sáng tạo
Đề kiểm tra 15 phút Toán 11 chân trời sáng tạo
Phiếu học tập theo bài Toán 11 chân trời sáng tạo cả năm
Trắc nghiệm đúng sai Toán 11 chân trời sáng tạo cả năm
Trắc nghiệm dạng câu trả lời ngắn Toán 11 chân trời sáng tạo cả năm
TÀI LIỆU GIẢNG DẠY TOÁN 11 CÁNH DIỀU
Giáo án toán 11 cánh diều đủ cả năm
Giáo án điện tử toán 11 cánh diều
Giáo án chuyên đề Toán 11 cánh diều đủ cả năm
Giáo án điện tử chuyên đề toán 11 cánh diều
Giáo án dạy thêm toán 11 cánh diều đủ cả năm
Giáo án powerpoint dạy thêm toán 11 cánh diều đủ cả năm
Trò chơi khởi động Toán 11 cánh diều
Câu hỏi và bài tập trắc nghiệm toán 11 cánh diều
Đề thi toán 11 cánh diều
File word đáp án toán 11 cánh diều
Bài tập file word Toán 11 Cánh diều
Kiến thức trọng tâm Toán 11 cánh diều
Đề kiểm tra 15 phút Toán 11 cánh diều
Phiếu học tập theo bài Toán 11 cánh diều cả năm
Trắc nghiệm đúng sai Toán 11 cánh diều cả năm
Trắc nghiệm dạng câu trả lời ngắn Toán 11 cánh diều cả năm
