Giáo án và PPT Toán 11 chân trời Bài 2: Các quy tắc tính đạo hàm
Đồng bộ giáo án word và powerpoint (ppt) Bài 2: Các quy tắc tính đạo hàm. Thuộc chương trình Toán 11 chân trời sáng tạo. Giáo án được biên soạn chỉn chu, hấp dẫn. Nhằm tạo sự lôi cuốn và hứng thú học tập cho học sinh.
Click vào ảnh dưới đây để xem giáo án WORD rõ nét












Giáo án ppt đồng bộ với word










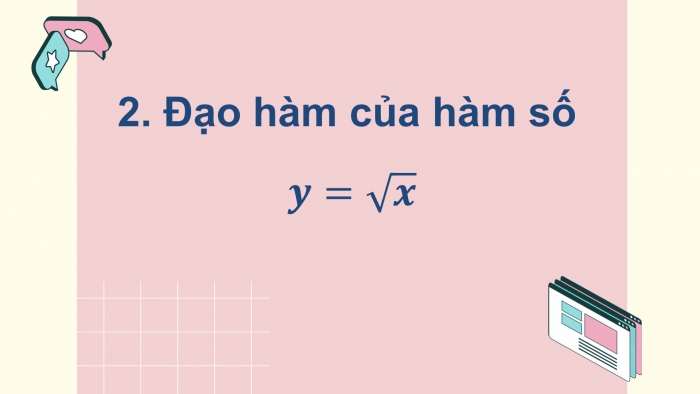

Còn nữa....
Các tài liệu bổ trợ khác
Xem toàn bộ: Trọn bộ giáo án và PPT Toán 11 chân trời sáng tạo
BÀI 2. CÁC QUY TẮC ĐẠO HÀM (5 TIẾT)
HOẠT ĐỘNG KHỞI ĐỘNG
GV yêu cầu HS thảo luận và trả lời:
Giả sử hàm số f(x) và g(x) lần lượt có đạo hàm tại x0 là f'(x0) và g'(x0). Làm thế nào để tính đạo hàm của các hàm số là tổng, hiệu, tích hoặc thương của f(x) và g(x) tại x0?
Ví dụ: Hãy tính đạo hàm của hàm số: C + ![]() ?
?
- GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC
1. ĐẠO HÀM CỦA HÀM SỐ ![]()
Hoạt động 1: Tìm hiểu đạo hàm của hàm số ![]()
- GV yêu cầu HS nhắc lại cách tính đạo hàm bằng định nghĩa.
- GV yêu cầu HS thảo luận nhóm đôi, hoàn thành HĐKP 1.
+ Dự đoán đạo hàm của hàm số y = xn.
- GV nhận xét, chốt đáp án, từ kết quả đó giới thiệu quy tắc tính đạo hàm của hàm số trên.
- HS đọc hiểu Ví dụ 1.
- GV cho HS làm bài độc lập hoàn thành phần HĐTH 1.
- GV mời 1 HS lên bảng trình bày.
Sản phẩm dự kiến:
Nhắc lại lí thuyết
Cho hàm số ![]() xác định trên khoảng
xác định trên khoảng ![]() và
và ![]() .
.
Nếu tồn tại giới hạn hữu hạn

Thì giới hạn này được gọi là đạo hàm của hàm số f(x) tại ![]() , kí hiệu là
, kí hiệu là ![]() hoặc
hoặc ![]() .
.
Vậy: ![]() .
.
HĐKP 1:
a) Ta có:
![]() .
.
Vậy ta có: ![]() .
.
b) Từ kết quả bài trước ta có:
![]()
Dự đoạn: ![]()
Quy tắc
Hàm số ![]() với
với ![]() có đạo hàm trên
có đạo hàm trên ![]() và
và ![]() .
.
Ví dụ 1 (SGK – Tr.42)
Thực hành 1
Ta có: ![]()
Khi đó:
![]()
2. ĐẠO HÀM CỦA HÀM SỐ Y = ![]()
Hoạt động 2: Tìm hiểu đạo hàm của hàm số y = ![]()
- GV yêu cầu HS thảo luận nhóm đôi, hoàn thành HĐKP 2.
- GV mới 1 HS lên bảng trình bày.
- GV nhận xét, chốt đáp án, giới thiệu quy tắc tính đạo hàm của hàm căn thức.
- GV lưu ý với HS: “Trong công thức có chứa ![]() dưới mẫu số, do đó xo > 0”
dưới mẫu số, do đó xo > 0”
- HS đọc hiểu Ví dụ 2.
- GV cho HS làm bài độc lập hoàn thành phần HĐTH 2.
- GV mời 1 HS lên bảng trình bày.
- GV đặt câu hỏi đưa ra nhận xét.
+ Cho hàm số y = xα, α là số thực. Hãy tính đạo hàm của hàm số đó. Tính đạo hàm của hàm số khi α = ![]()
+ Nhắc lại các kết quả của bài trước khi tính đạo hàm của C (C là hằng số) và ![]()
- HS đọc hiểu Ví dụ 3.
- GV cho HS làm bài độc lập hoàn thành phần HĐTH 3.
- GV mời 1 HS lên bảng trình bày.
Sản phẩm dự kiến:
HĐKP 2:
Ta có: 
![]()
Vậy ![]() .
.
Quy tắc
Hàm số ![]() có đạo hàm trên khoảng
có đạo hàm trên khoảng ![]() và
và ![]() .
.
Ví dụ 2 (SGK – Tr.43)
Thực hành 2
Ta có: ![]()
Hệ số góc của tiếp tuyến tại điểm có hoành độ bằng 4 là:
![]() .
.
Với ![]() thì
thì ![]() .
.
Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ bằng 4 là:

Nhận xét
a) Cho số thực ![]() . Hàm số
. Hàm số ![]() được gọi là hàm số lũy thừa ( với tập xác định
được gọi là hàm số lũy thừa ( với tập xác định ![]() ).
).
Ta có: ![]()
Với ![]() ta nhận được:
ta nhận được:

b) Ta có: ![]() ;
; ![]() .
.
Ví dụ 3 (SGK – Tr.43)
Thực hành 3.
a) Ta có: ![]() .
.
Khi đó ![]() .
.
b) Ta có: ![]() .
.
Khi đó 
3. ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC
Hoạt động 3: Tìm hiểu đạo hàm của hàm số lượng giác
- GV yêu cầu HS thảo luận nhóm đôi, hoàn thành HĐKP 3.
+ Tính đạo hàm của hàm số y = sin x cho biết ![]()
- GV gọi 1 HS trình bày bài.
- GV giao thêm nhiệm vụ cho nhóm:
+ Áp dụng định nghĩa tính đạo hàm của các hàm số: cos x; tan x; cot x.
- Từ kết quả của hoạt động trên, GV giới thiệu quy tắc tính đạo hàm của hàm số lượng giác.
- HS đọc hiểu Ví dụ 4.
- GV cho HS làm bài độc lập hoàn thành phần HĐTH 4.
- GV mời 1 HS lên bảng trình bày.
Sản phẩm dự kiến:
HĐKP 3
Ta có:
![]()


![]()
Vậy ![]() .
.
Quy tắc
Ví dụ 4 (SGK – tr.44)
Thực hành 4
Ta có: ![]() .
.
Vậy  .
.
4. ĐẠO HÀM
Hoạt động 4: Tìm hiểu đạo hàm
- GV yêu cầu HS thảo luận nhóm đôi, hoàn thành HĐKP 4.
+ Áp dụng định nghĩa tính đạo hàm của hàm số y = ex cho biết ![]() = 1
= 1
+ Áp dụng định nghĩa tính đạo hàm của hàm số y = ln x cho biết ![]()
- GV đặt câu hỏi mở rộng:
+ Tính đạo hàm của hàm số y = ax.
+ Tính đạo hàm của hàm số y = loga x
(Gợi ý: Sử dụng ax = exln a; loga x = ![]() , sau đó áp dụng định nghĩa để tính.)
, sau đó áp dụng định nghĩa để tính.)
- GV tổng kết, giới thiểu quy tắc tính đạo hàm của hàm số mũ và hàm số lôgarit.
- HS đọc và trình bày Ví dụ 5.
- GV cho HS làm bài độc lập hoàn thành phần HĐTH 5.
- GV mời 2 HS lên bảng trình bày.
Sản phẩm dự kiến:
HĐKP 4
a) Ta có:
![]()
![]()
Vậy ![]() .
.
b)  .
.  .
.
Vậy ![]() .
.
Quy tắc
Ví dụ 5 (SGK – tr.44)
Thực hành 5
a) Ta có: ![]()
Khi đó ![]() .
.
b) Ta có: ![]() .
.
Khi đó ![]() .
.
5. ĐẠO HÀM CỦA TỔNG, HIỆU, TÍCH, THƯƠNG CỦA HAI HÀM SỐ
Hoạt động 5: Tìm hiểu đạo hàm của tổng, hiệu, tích, thương của hai hàm số
- GV yêu cầu HS thảo luận nhóm đôi, hoàn thành HĐKP 5.
- Từ kết quả của hoạt động trên, GV giới thiệu quy tắc tính đạo hàm của tông, hiệu, tích, thương của hai hàm số.
- GV đặt câu hỏi mở rộng:
+ Nếu u = c (c là hằng số) thì công thức (1) được biểu thị như thế nào?
+ Nếu u = 1 thì công thức (2) được biểu thị như thế nào?
- HS đọc hiểu ví dụ 6.
- HS đọc hiểu ví dụ 7.
- GV cho HS làm bài độc lập hoàn thành phần HĐTH 6.
- GV mời 2 HS lên bảng trình bày.
Sản phẩm dự kiến:
HĐKP 5



![]() .
.
Vậy ![]() .
.
Quy tắc
Cho hai hàm số ![]() có đạo hàm tại điểm
có đạo hàm tại điểm ![]() thuộc tập xác định. Ta có:
thuộc tập xác định. Ta có:


 (1)
(1) (với
(với  (2)
(2)
Chú ý:
- Với
 (
( là hằng số), ta có:
là hằng số), ta có: 
- Với
 , ta có:
, ta có:  (với
(với  .
.
Ví dụ 6 (SGK – tr.45)
Ví dụ 7 (SGK – tr.45)
Thực hành 6
a) Ta có: ![]()
b) Ta có: ![]()
6. ĐẠO HÀM CỦA HÀM HỢP
Hoạt động 6: Tìm hiểu đạo hàm của hàm hợp
- GV yêu cầu HS hoàn thành HĐKP 6.
- GV nhận xét, giới thiệu định nghĩa hàm hợp.
- HS tìm hiểu Ví dụ 8, GV gọi 2 HS đứng tại chỗ trình bày lại.
- GV giới thiệu quy tắc tính đạo hàm của hàm hợp.
- HS tìm hiểu Ví dụ 9, GV gọi 3 HS đứng tại chỗ trình bày lại.
- GV cho HS làm bài độc lập hoàn thành phần HĐTH 7.
- GV mời 2 HS lên bảng trình bày.
- HS tìm hiểu bảng đạo hàm.
Sản phẩm dự kiến:
HĐKP 6
a) Ta có: ![]() .
.
b) Ta có: ![]()
![]() .
.
![]() .
.
![]() .
.
Có ![]()
Vậy ta có: ![]() .
.
Định nghĩa hàm hợp
Cho ![]() là hàm số của
là hàm số của ![]() xác định trên khoảng
xác định trên khoảng ![]() và lấy giá trị trên khoảng
và lấy giá trị trên khoảng ![]() ;
; ![]() là hàm số của
là hàm số của ![]() xác định trên khoảng
xác định trên khoảng ![]() và lấy giá trị trên
và lấy giá trị trên ![]() . Ta lập hàm số xác định trên
. Ta lập hàm số xác định trên ![]() và lấy giá trị trên
và lấy giá trị trên ![]() theo quy tắc sau:
theo quy tắc sau: ![]() .
.
Hàm số ![]() được gọi là hàm hợp của hàm số
được gọi là hàm hợp của hàm số ![]() với
với ![]() .
.

Ví dụ 8 (SGK – Tr.46)
Quy tắc
Cho hàm số ![]() có đạo hàm tại
có đạo hàm tại ![]() là
là ![]() và hàm số
và hàm số ![]() có đạo hàm
có đạo hàm ![]() là
là ![]() thì hàm hợp
thì hàm hợp ![]() có đạo hàm tại
có đạo hàm tại ![]() là
là ![]() .
.
Ví dụ 9 (SGK – tr.46)
Thực hành 7
a) ![]() .
.
b) ![]() .
.
c) ![]() .
.
Bảng đạo hàm (SGK – Tr.47)
7. ĐẠO HÀM CẤP HAI
Hoạt động 7: Tìm hiểu đạo hàm cấp hai
- GV yêu cầu HS hoàn thành HĐKP 7.
- GV giới thiệu đạo hàm cấp hai.
- HS tìm hiểu Ví dụ 10.
- GV đặt câu hỏi gợi mở: “Vậy đạo hàm cấp hai được áp dụng tính đại lượng nào trong vật lý?”. Từ đó đưa ra ý nghĩa cơ học của đạo hàm cấp hai.
- HS tìm hiểu Ví dụ 11.
- GV cho HS làm bài độc lập hoàn thành phần HĐTH 8.
- GV mời 2 HS lên bảng trình bày.
- GV cho HS làm bài độc lập hoàn thành phần Vận dụng.
+ Vận tốc của hòn sỏi tại thời điểm t là gì?
+ Gia tốc của hòn sỏi tại thời điểm t là gì?
- GV mời 1 HS lên bảng trình bày.
Sản phẩm dự kiến:
HĐKP 7:
a) Vận tốc tức thời tại thời điểm ![]() là:
là:
![]() .
.
b) ![]()
Gia tốc của chuyển động tại thời điểm ![]() là:
là: ![]() .
.
Định nghĩa
Cho hàm số ![]() có đạo hàm
có đạo hàm ![]() tại mọi
tại mọi ![]() .
.
Nếu hàm số ![]() có đạo hàm tại
có đạo hàm tại ![]() thì ta gọi đạo hàm của
thì ta gọi đạo hàm của ![]() là đạo hàm cấp hai của hàm số
là đạo hàm cấp hai của hàm số ![]() tại
tại ![]() , kí hiệu
, kí hiệu ![]() hoặc
hoặc ![]() .
.
Ví dụ 10 (SGK – Tr.48)
Ý nghĩa cơ học của đạo hàm cấp hai
Đạo hàm cấp hai ![]() là gia tốc tức thời tại thời điểm
là gia tốc tức thời tại thời điểm ![]() của vật chuyển động có phương trình
của vật chuyển động có phương trình ![]() .
.
Ví dụ 11 (SGK – Tr.48)
Thực hành 8
a) Ta có: ![]() .
.
Có ![]()
Vậy ![]() .
.
b) Ta có: ![]() .
.
![]()
Vậy ![]()
Vận dụng
Vận tốc của hòn sỏi tại thời điểm ![]() là:
là:
![]()
Gia tốc của hòn sỏi tại thời điểm ![]() là:
là:
![]()
Gia tốc rơi của hòn sỏi lúc ![]() là
là ![]() .
.
HOẠT ĐỘNG LUYỆN TẬP
Câu 1: Tính đạo hàm của hàm số f(x) = - x4 + 4x3 - 3x2 + 1 tại điểm x = -1.
A. f '(- 1) = 4
B. f '(- 1) = 14
C. f '(- 1) = 15
D. f '(- 1) = 24
Câu 2: Tính đạo hàm của hàm số y = (x3 - 2x2)2
A. f '(x) = 6x5 - 20x4 + 16x3
B. f '(x) = 6x5 + 16x3
C. f '(x) = 6x5 - 20x4 + 4x3
D. f '(x) = 6x5 - 20x4 - 16x3
Câu 3: Tính đạo hàm của hàm số y = (x2 - 2)(2x - 1)
A. y' = 4x
B. y' = 3x2 - 6x + 2
C. y' = 2x2 - 2x + 4
D. y' = 6x2 - 2x - 4
Sản phẩm dự kiến:
Câu 1: C
Câu 2: A
Câu 3: D
HOẠT ĐỘNG VẬN DỤNG
Vận dụng kiến thức, GV yêu cầu HS trả lời câu hỏi:
Câu 1: Một công ty xác định rằng tổng chi phí của họ, tính theo nghìn đô-la, để sản xuất x mặt hàng là C(x) = ![]() và công ty lên kế hoạch nâng sản lượng trong t tháng kể từ nay theo hàm số x(t) = 20t + 40. Chi phí sẽ tăng nhanh thế nào sau 4 tháng kể từ khi công ty thực hiện kế hoạch đó?
và công ty lên kế hoạch nâng sản lượng trong t tháng kể từ nay theo hàm số x(t) = 20t + 40. Chi phí sẽ tăng nhanh thế nào sau 4 tháng kể từ khi công ty thực hiện kế hoạch đó?
Câu 2: Trên Mặt Trăng, quãng đường rơi tự do của một vật được cho bởi công thức s(t) = 0,81t2, trong đó t là thời gian được tính bằng giây và s tính bằng mét. Một vật được thả rơi từ độ cao 200 m phía trên Mặt Trăng. Tại thời điểm t = 2 sau khi thả vật đó, tính:
a) Quãng đường vật đã rơi;
b) Gia tốc của vật.
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Trọn bộ giáo án và PPT Toán 11 chân trời sáng tạo
TÀI LIỆU GIẢNG DẠY TOÁN 11 KẾT NỐI TRI THỨC
Giáo án toán 11 kết nối tri thức đủ cả năm
Giáo án điện tử toán 11 kết nối tri thức
Giáo án chuyên đề Toán 11 kết nối tri thức đủ cả năm
Giáo án điện tử chuyên đề toán 11 kết nối tri thức
Giáo án dạy thêm toán 11 kết nối tri thức đủ cả năm
Giáo án powerpoint dạy thêm toán 11 kết nối tri thức đủ cả năm
Trò chơi khởi động Toán 11 kết nối tri thức
Video AI khởi động Toán 11 kết nối tri thức hấp dẫn
Câu hỏi và bài tập trắc nghiệm toán 11 kết nối tri thức
Đề thi toán 11 kết nối tri thức
File word đáp án toán 11 kết nối tri thức
Bài tập file word Toán 11 kết nối tri thức
Kiến thức trọng tâm Toán 11 kết nối tri thức
Đề kiểm tra 15 phút Toán 11 kết nối tri thức
Phiếu học tập theo bài Toán 11 kết nối tri thức cả năm
Trắc nghiệm đúng sai Toán 11 kết nối tri thức cả năm
Trắc nghiệm dạng câu trả lời ngắn Toán 11 kết nối tri thức cả năm
TÀI LIỆU GIẢNG DẠY TOÁN 11 CHÂN TRỜI SÁNG TẠO
Giáo án toán 11 chân trời sáng tạo đủ cả năm
Giáo án điện tử toán 11 chân trời sáng tạo
Giáo án chuyên đề Toán 11 chân trời sáng tạo đủ cả năm
Giáo án điện tử chuyên đề Toán 11 chân trời sáng tạo
Giáo án dạy thêm toán 11 chân trời sáng tạo đủ cả năm
Giáo án powerpoint dạy thêm toán 11 chân trời sáng tạo đủ cả năm
Trò chơi khởi động Toán 11 chân trời sáng tạo
Video AI khởi động Toán 11 chân trời sáng tạo hấp dẫn
Câu hỏi và bài tập trắc nghiệm toán 11 chân trời sáng tạo
Đề thi toán 11 chân trời sáng tạo
File word đáp án toán 11 chân trời sáng tạo
Bài tập file word toán 11 chân trời sáng tạo
Kiến thức trọng tâm Toán 11 chân trời sáng tạo
Đề kiểm tra 15 phút Toán 11 chân trời sáng tạo
Phiếu học tập theo bài Toán 11 chân trời sáng tạo cả năm
Trắc nghiệm đúng sai Toán 11 chân trời sáng tạo cả năm
Trắc nghiệm dạng câu trả lời ngắn Toán 11 chân trời sáng tạo cả năm
TÀI LIỆU GIẢNG DẠY TOÁN 11 CÁNH DIỀU
Giáo án toán 11 cánh diều đủ cả năm
Giáo án điện tử toán 11 cánh diều
Giáo án chuyên đề Toán 11 cánh diều đủ cả năm
Giáo án điện tử chuyên đề toán 11 cánh diều
Giáo án dạy thêm toán 11 cánh diều đủ cả năm
Giáo án powerpoint dạy thêm toán 11 cánh diều đủ cả năm
Trò chơi khởi động Toán 11 cánh diều
Video AI khởi động Toán 11 cánh diều hấp dẫn
Câu hỏi và bài tập trắc nghiệm toán 11 cánh diều
Đề thi toán 11 cánh diều
File word đáp án toán 11 cánh diều
Bài tập file word Toán 11 Cánh diều
Kiến thức trọng tâm Toán 11 cánh diều
Đề kiểm tra 15 phút Toán 11 cánh diều
Phiếu học tập theo bài Toán 11 cánh diều cả năm
Trắc nghiệm đúng sai Toán 11 cánh diều cả năm
Trắc nghiệm dạng câu trả lời ngắn Toán 11 cánh diều cả năm
