Giáo án và PPT Toán 11 chân trời Bài 3: Hàm số mũ. Hàm số lôgarit
Đồng bộ giáo án word và powerpoint (ppt) Bài 3: Hàm số mũ. Hàm số lôgarit. Thuộc chương trình Toán 11 chân trời sáng tạo. Giáo án được biên soạn chỉn chu, hấp dẫn. Nhằm tạo sự lôi cuốn và hứng thú học tập cho học sinh.
Click vào ảnh dưới đây để xem giáo án WORD rõ nét









Giáo án ppt đồng bộ với word











Còn nữa....
Các tài liệu bổ trợ khác
Xem toàn bộ: Trọn bộ giáo án và PPT Toán 11 chân trời sáng tạo
BÀI 3. HÀM SỐ MŨ. HÀM SỐ LÔGARIT (2 TIẾT)
HOẠT ĐỘNG KHỞI ĐỘNG
- GV yêu cầu HS đọc tình huống mở đầu thảo luận và trả lời:
Chuyện kể rằng, ngày xưa ở xứ Ấn Độ, người phát minh ra bàn cờ vua được nhà vua cho phép từ chọn phần thưởng là những hạt thóc đặt vào 64 ô của bàn cờ theo quy tắc như sau: 1 hạt thóc ở ô thứ nhất, 2 hạt thóc ở ô thứ hai, 4 hạt thóc ở ô thứ ba,…. Cứ như thế số hạt thóc ở ô sau gấp đôi số hạt thóc ở ô trước. Nhà vua nhanh chóng chấp nhận lời đề nghị, vì cho rằng phần thưởng như vậy thì quá dễ dàng.

Tuy nhiên, theo phần thưởng này, tổng số hạt thóc có trong 64 ô là 264 – 1, tính ra được hơn 18.1018 hạt thóc, hay hơn 450 tỉ tấn thóc (mỗi hạt thóc nặng khoảng 25 mg). Nhà vua không thể đủ thóc thưởng cho nhà phát minh.
Từ tình huống trên, có nhận xét gì về giá trị của biểu thức 2x khi x trở nên lớn?
- GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC
1. HÀM SỐ MŨ
Hoạt động 1: Tìm hiểu hàm số mũ
- GV giới thiệu y = 2x gọi là hàm số mũ khi cho tương ứng mỗi số thực x thì được số thực y = 2x.
- HS khái quát thế nào là hàm số mũ. Chú ý về điều kiện của cơ số α.
- GV đặt câu hỏi: hàm số y = ax có tập xác định là gì?
- HS đọc và giải thích Ví dụ 1, dựa vào khái niệm hàm số mũ.
- HS thực hiện HĐKP 2 theo nhóm đôi. GV hướng dẫn:
a) ii)
+ Đồ thị là đường liền hay đường drt?
+ Đồ thị có hướng đi như thế nào? Đi lên hay đi xuống khi x tăng dần? (Đi lên khi đi từ trái qua phải).
+ Đồ thị gần như dốc thẳng đứng khi càng sang phía bên phải
+ Càng sang phía bên trái, đổ thị càng tiến sát đến phía nào của trục hoành?
+ Thực hiện tương tự với đồ thị hàm số y = ![]()
+ Nhận thấy với a > 1 và a < 1 thì tính chất hàm số có sự thay đổi.
- Từ đó tổng quát các dạng đô thị hàm số y = ax và tính chất của hàm số.
- HS đọc, trình bày Ví dụ 2, 3
+ VD2: dựa vào việc xác định cơ số a > 1 hoặc a < 1 và so sánh số mũ.
+ VD3: tính giá trị hàm mũ.
- HS thực hiện Thực hành 1, 2.
+ Thực hành 1: GV có thê cho HS nhận xét về tính đối xứng của đồ thị hai hàm số và giải thích lí do.
+ Thực hành 2: HS so sánh tương tự ví dụ 2.
- HS làm Vận dụng 1.
+ Để tính khối lượng vi khuẩn sau thời gian t nào đó, ta làm thế nào?
Sản phẩm dự kiến:
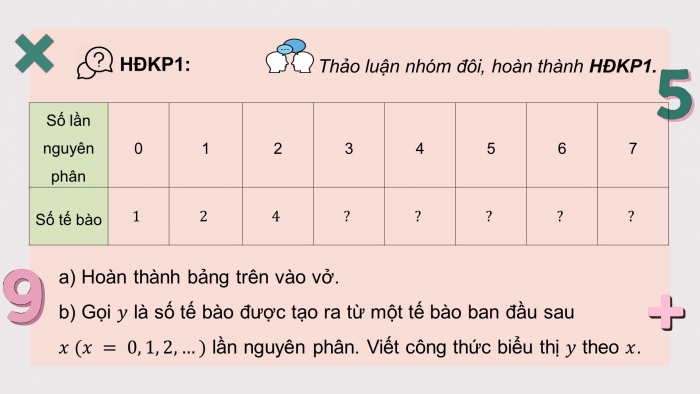
HĐKP 1
a)
Số lần nguyên phân | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Số tế bào |
|
|
|
|
|
|
|
|
b) ![]() .
.
Kết luận
Cho số thực dương ![]() khác 1.
khác 1.
Hàm số cho tương ứng mỗi số thực ![]() với số thực
với số thực ![]() được gọi là hàm số mũ cơ số
được gọi là hàm số mũ cơ số ![]() , kí hiệu
, kí hiệu ![]()
Nhận xét: Hàm số ![]() có tập xác định
có tập xác định ![]() .
.
Ví dụ 1 (SGK-tr.20)
*) Đồ thị của hàm số mũ
HĐKP 2
a) i)
| -2 | -1 | 0 | 1 | 2 |
|
|
| 1 | 2 | 4 |
ii) Hàm số ![]() liên tục trên
liên tục trên ![]() (đồ thị là đường liền); đồng biến trên
(đồ thị là đường liền); đồng biến trên ![]() (đồ thị đi lên khi đi từ trái qua phải);
(đồ thị đi lên khi đi từ trái qua phải);
![]() ;
; ![]() ;
;
Tập giá trị ![]() .
.
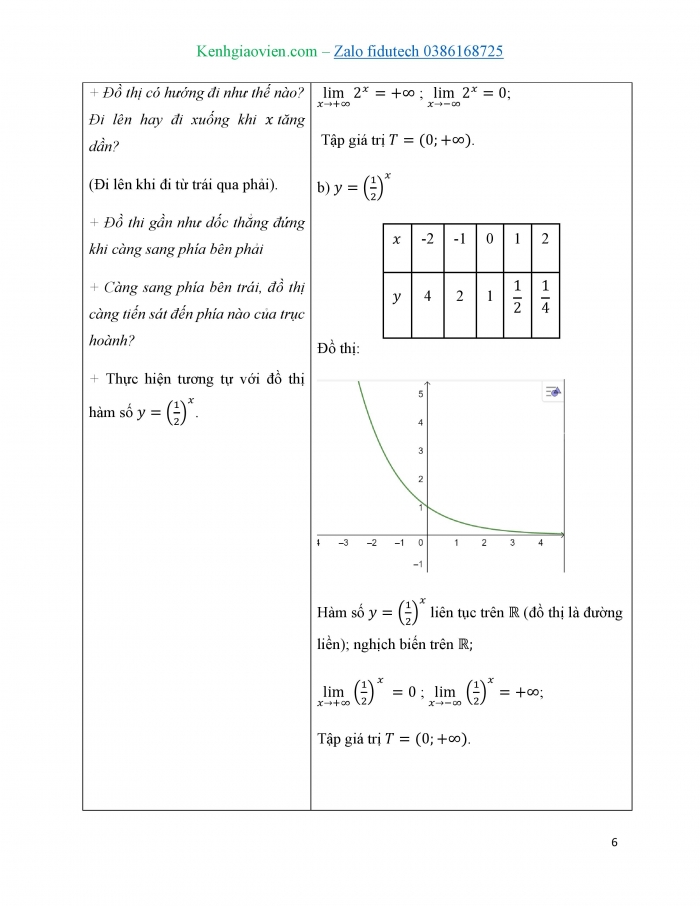
b) ![]()
| -2 | -1 | 0 | 1 | 2 |
| 4 | 2 | 1 |
|
|
Đồ thị:

Hàm số ![]() liên tục trên
liên tục trên ![]() (đồ thị là đường liền); nghịch biến trên
(đồ thị là đường liền); nghịch biến trên ![]()
![]() ;
; ![]() ;
;
Tập giá trị ![]() .
.
Tổng quát:

Hàm số ![]() có:
có:
(1) Tập xác định: ![]() .
.
Tập giá trị: ![]() .
.
Hàm số liên tục trên ![]() .
.
(2) Sự biến thiên:
- Nếu
 thì hàm số đồng biến trên
thì hàm số đồng biến trên  và
và
![]()
- Nếu
 thì hàm số nghịch biến trên
thì hàm số nghịch biến trên  và
và
![]() .
.
(3) Đồ thị:
- Cắt trục tung tại điểm
 ; đi qua điểm
; đi qua điểm  .
. - Nằm phía trên trục hoành
Ví dụ 2 (SGK -tr.21)
Ví dụ 3 (SGK -tr.21)
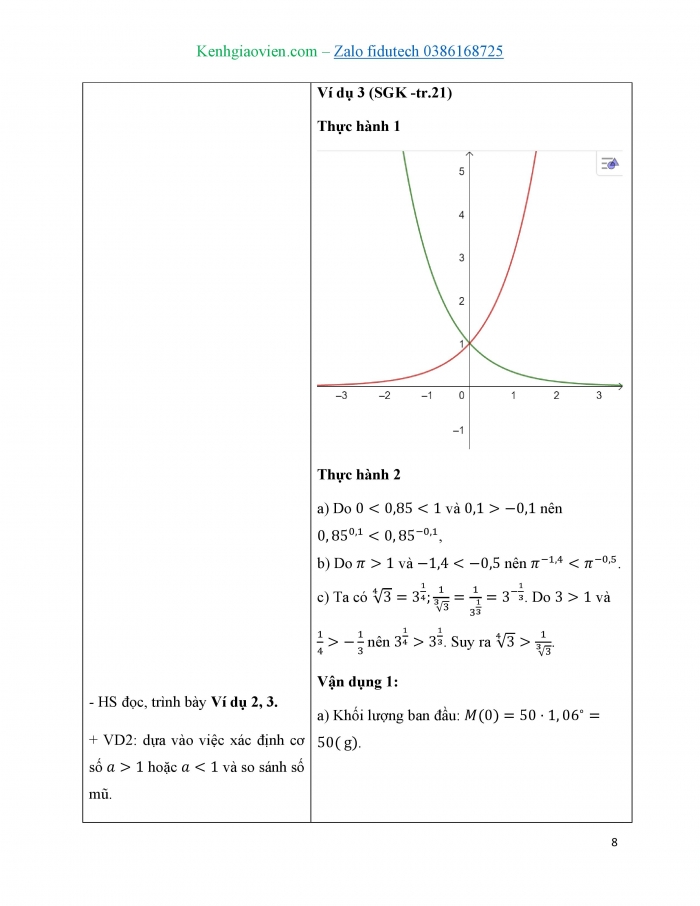
Thực hành 1

Thực hành 2
a) Do ![]() và
và ![]() nên
nên ![]() ,
,
b) Do ![]() và
và ![]() nên
nên ![]() .
.
c) Ta có  . Do
. Do ![]() và
và ![]() nên
nên ![]() . Suy ra
. Suy ra ![]() .
.
Vận dụng 1:
a) Khối lượng ban đầu: ![]() .
.
b) Khối lượng vi khuẩn sau 2 giờ: ![]() ;
;
Khối lượng vi khuẩn sau 10 giờ: ![]() .
.
c) Do ![]() nên nếu
nên nếu ![]() thì
thì ![]() , suy ra
, suy ra ![]() hay
hay ![]() . Vậy khối lượng vi khuẩn của mẻ nuôi cấy tăng dần theo thời gian.
. Vậy khối lượng vi khuẩn của mẻ nuôi cấy tăng dần theo thời gian.
2. HÀM SỐ LÔGARIT
Hoạt động 2: Tìm hiểu hàm số lôgarit
- GV yêu cầu hoàn thành HĐKP 3:
- GV giới thiệu y = logax gọi là hàm số lôgarit khi cho tương ứng mỗi số thực x thì được số thực y = logax
- HS khái quát thế nào là hàm số lôgarit. Chú ý về điều kiện của cơ số a.
- GV đặt câu hỏi: hàm số y = logax có tập xác định là gì?
- HS đọc, trình bày Ví dụ 4, giải thích dựa khái niệm hàm số lôgarit.
- HS làm HĐKP 4 theo nhóm đôi.
+ a) ii)
+ Đồ thị là đường liền hay đường đứt?
+ Đồ thị có hướng đi như thế nào? Đi lên hay đi xuống khi x tăng dần? (Đi lên khi đi từ trái qua phải).
+ Khi x giảm dần đến 0 thì giá trị của y tiến đến đâu?
+ Thực hiện tương tự với đồ thị hàm số y = ![]() .
.
+ Nhận thấy với a > 1 và a < 1 thì tính chất hàm số có sự thay đổi.
- Từ đó tổng quát các dạng đồ thị hàm số y = loga x và tính chất của hàm số.
- HS đọc và giải thích Ví dụ 5, 6.
- HS làm Thực hành 3, 4.
+ Nhận xét tính đối xứng của đồ thị ở Thực hành 3, giải thích.
- HS thực hiện Vận dụng 2.
Sản phẩm dự kiến:
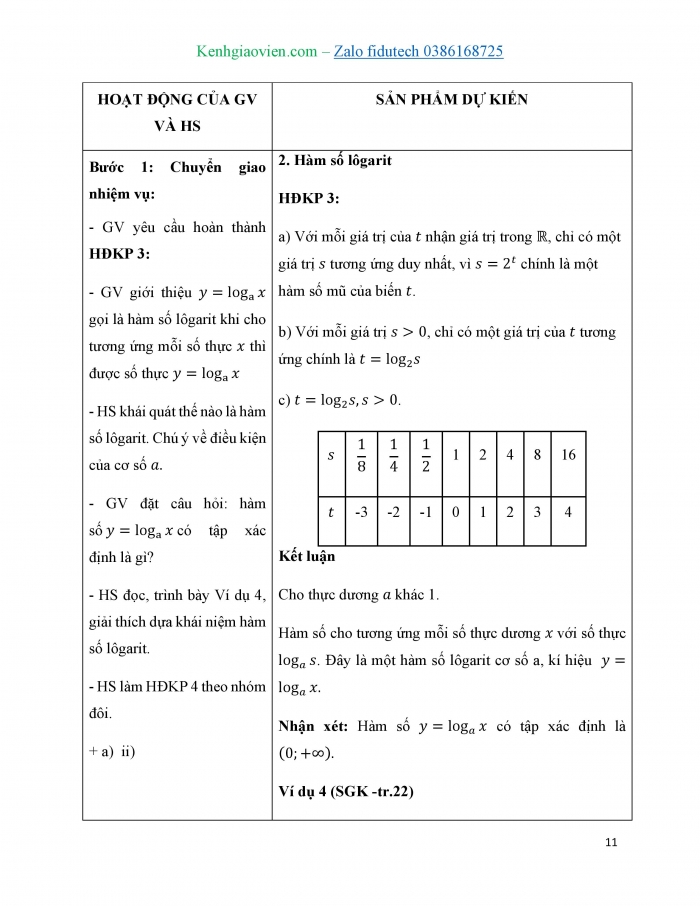
HĐKP 3:
a) Với mỗi giá trị của ![]() nhận giá trị trong
nhận giá trị trong ![]() , chỉ có một giá trị
, chỉ có một giá trị ![]() tương ứng duy nhất, vì
tương ứng duy nhất, vì ![]() chính là một hàm số mũ của biến
chính là một hàm số mũ của biến ![]() .
.
b) Với mỗi giá trị ![]() , chỉ có một giá trị của
, chỉ có một giá trị của ![]() tương ứng chính là
tương ứng chính là ![]()
c) ![]() .
.
|
|
|
| 1 | 2 | 4 | 8 | 16 |
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
Kết luận
Cho thực dương ![]() khác 1.
khác 1.
Hàm số cho tương ứng mỗi số thực dương ![]() với số thực
với số thực ![]() . Đây là một hàm số lôgarit cơ số a, kí hiệu
. Đây là một hàm số lôgarit cơ số a, kí hiệu ![]()
Nhận xét: Hàm số ![]() có tập xác định là
có tập xác định là ![]()
Ví dụ 4 (SGK -tr.22)
*) Đồ thị hàm số lôgarit
HĐKP 4
a) i)
|
| 1 | 2 | 4 |
| -1 | 0 | 1 | 2 |
ii) Hàm số ![]() liên tục trên
liên tục trên ![]() ; đồng biến trên
; đồng biến trên ![]()
![]() ;
;
Tập giá trị ![]() .
.
b) Hàm số ![]() liên tục trên
liên tục trên ![]() ; nghịch biến trên
; nghịch biến trên ![]()
![]() ;
;
Tập giá trị ![]() .
.
Tổng quát
Đồ thị của hàm số ![]() với
với ![]() và
và ![]()

Kết luận: Hàm số ![]()
(1) Tập xác định: ![]() . Tập giá trị:
. Tập giá trị: ![]() . Hàm số liên tục trên
. Hàm số liên tục trên ![]() .
.
(2) Sự biến thiên:
- Nếu
 thì hàm số đồng biến trên
thì hàm số đồng biến trên  và
và
![]() .
.
- Nếu
 thì hàm số nghịch biến trên
thì hàm số nghịch biến trên  và
và
![]()
(3) Đồ thị:
- Cắt trục hoành tại điểm
 , đi qua điểm
, đi qua điểm 
- Nằm bên phải trục tung.
Ví dụ 5 (SGK -tr.24)
Ví dụ 6 (SGK -tr.24)
Thực hành 3

Thực hành 4
a) Do ![]() và
và ![]() nên
nên ![]() ;
;
b) ![]() .
.
Do ![]() và
và ![]() nên
nên ![]() . Suy ra
. Suy ra ![]() .
.
c)  .
.
Do ![]() và
và ![]() nên
nên ![]() . Suy ra
. Suy ra ![]() .
.
Vận dụng 2
a) ![]() .
.
b) Âm thanh có cường độ âm không vượt quá ![]() thì có mức cường độ âm
thì có mức cường độ âm ![]() . Vậy để nghe trong thời gian dài mà không gây hại cho tai, âm thanh phải có mức cường độ âm không vượt quá 70 dB.
. Vậy để nghe trong thời gian dài mà không gây hại cho tai, âm thanh phải có mức cường độ âm không vượt quá 70 dB.
HOẠT ĐỘNG LUYỆN TẬP
Câu 1: Cho a > 0 a ne1 Tìm mệnh đề đúng trong các mệnh đề sau:
A. Tập xác định của hàm số y = ax là khoảng (0; +∞)
B. Tập giá trị của hàm số y = logax là tập R.
C. Tập xác định của hàm số y = logax là tập R.
D. Tập giá trị của hàm số y = ax là tập R
Câu 2: Trong các hàm số sau, hàm số nào đồng biến trên tập xác định của nó?
A. y = (2016)2x
B. y = (0, 1)2x
C. y = ![]()
D. y = ![]()
Câu 3: Tập xác định D của hàm số y = ![]()
A. D = (- 1; 3)
B. D= (- ∞; - 1) ∪ (3; + ∞)
C. D = [- 1; 3]
D. D= (- ∞; - 1] ∪ [3;+ ∞)
Sản phẩm dự kiến:
Câu 1: B
Câu 2: A
Câu 3: B
HOẠT ĐỘNG VẬN DỤNG
Vận dụng kiến thức, GV yêu cầu HS trả lời câu hỏi:
Câu 1: Cường độ ánh sáng I dưới mặt biển giảm dần theo độ sâu theo công thức I = I0.ad, trong đó I0 là cường độ ánh sáng tại mặt nước biển, a là hằng số (a > 0) và d là độ sâu tính bằng mét tính từ mặt nước biển.
(Nguồn: https://www.britannica.com/science/seawer/Optical-properties)
a) Có thể khẳng định rằng 0 < a < 1 không? Giải thích.
b) Biết rẳng cường độ ánh sáng tại độ sâu 1 m bằng 0,95I0. Tìm giá trị của a.
c) Tại độ sâu 20 m, cường độ ánh sáng bằng bao nhiêu phần trăm so với I0? (Làm tròn kết quả đến hàng đơn vị.)
Câu 2: Công thức h=−19,4.log ![]() là mô hình đơn giản cho phép tính độ cao h so với mặt nước biển của một vị trí trong không trung (tính bằng kilômét) theo áp suất không khí P tại điểm đó và áp suất P0 của không khí tại mặt nước biển (cùng tính bằng Pa – đơn vị áp suất, đọc là Pascal).
là mô hình đơn giản cho phép tính độ cao h so với mặt nước biển của một vị trí trong không trung (tính bằng kilômét) theo áp suất không khí P tại điểm đó và áp suất P0 của không khí tại mặt nước biển (cùng tính bằng Pa – đơn vị áp suất, đọc là Pascal).
(Nguồn: https://doi.org/10.1007/s40828-020-0111-6)
a) Nếu áp suất không khí ngoài máy bay bằng ![]() thì máy bay đang ở độ cao nào?
thì máy bay đang ở độ cao nào?
b) Áp suất không khí tại đỉnh của ngọn núi A bằng ![]() lần áp suất không khí tại đỉnh của ngọn núi B. Ngọn núi nào cao hơn và cao hơn bao nhiêu kilômét? (Làm tròn kết quả đến hàng phần mười.)
lần áp suất không khí tại đỉnh của ngọn núi B. Ngọn núi nào cao hơn và cao hơn bao nhiêu kilômét? (Làm tròn kết quả đến hàng phần mười.)
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Trọn bộ giáo án và PPT Toán 11 chân trời sáng tạo
TÀI LIỆU GIẢNG DẠY TOÁN 11 KẾT NỐI TRI THỨC
Giáo án toán 11 kết nối tri thức đủ cả năm
Giáo án điện tử toán 11 kết nối tri thức
Giáo án chuyên đề Toán 11 kết nối tri thức đủ cả năm
Giáo án điện tử chuyên đề toán 11 kết nối tri thức
Giáo án dạy thêm toán 11 kết nối tri thức đủ cả năm
Giáo án powerpoint dạy thêm toán 11 kết nối tri thức đủ cả năm
Trò chơi khởi động Toán 11 kết nối tri thức
Video AI khởi động Toán 11 kết nối tri thức hấp dẫn
Câu hỏi và bài tập trắc nghiệm toán 11 kết nối tri thức
Đề thi toán 11 kết nối tri thức
File word đáp án toán 11 kết nối tri thức
Bài tập file word Toán 11 kết nối tri thức
Kiến thức trọng tâm Toán 11 kết nối tri thức
Đề kiểm tra 15 phút Toán 11 kết nối tri thức
Phiếu học tập theo bài Toán 11 kết nối tri thức cả năm
Trắc nghiệm đúng sai Toán 11 kết nối tri thức cả năm
Trắc nghiệm dạng câu trả lời ngắn Toán 11 kết nối tri thức cả năm
TÀI LIỆU GIẢNG DẠY TOÁN 11 CHÂN TRỜI SÁNG TẠO
Giáo án toán 11 chân trời sáng tạo đủ cả năm
Giáo án điện tử toán 11 chân trời sáng tạo
Giáo án chuyên đề Toán 11 chân trời sáng tạo đủ cả năm
Giáo án điện tử chuyên đề Toán 11 chân trời sáng tạo
Giáo án dạy thêm toán 11 chân trời sáng tạo đủ cả năm
Giáo án powerpoint dạy thêm toán 11 chân trời sáng tạo đủ cả năm
Trò chơi khởi động Toán 11 chân trời sáng tạo
Video AI khởi động Toán 11 chân trời sáng tạo hấp dẫn
Câu hỏi và bài tập trắc nghiệm toán 11 chân trời sáng tạo
Đề thi toán 11 chân trời sáng tạo
File word đáp án toán 11 chân trời sáng tạo
Bài tập file word toán 11 chân trời sáng tạo
Kiến thức trọng tâm Toán 11 chân trời sáng tạo
Đề kiểm tra 15 phút Toán 11 chân trời sáng tạo
Phiếu học tập theo bài Toán 11 chân trời sáng tạo cả năm
Trắc nghiệm đúng sai Toán 11 chân trời sáng tạo cả năm
Trắc nghiệm dạng câu trả lời ngắn Toán 11 chân trời sáng tạo cả năm
TÀI LIỆU GIẢNG DẠY TOÁN 11 CÁNH DIỀU
Giáo án toán 11 cánh diều đủ cả năm
Giáo án điện tử toán 11 cánh diều
Giáo án chuyên đề Toán 11 cánh diều đủ cả năm
Giáo án điện tử chuyên đề toán 11 cánh diều
Giáo án dạy thêm toán 11 cánh diều đủ cả năm
Giáo án powerpoint dạy thêm toán 11 cánh diều đủ cả năm
Trò chơi khởi động Toán 11 cánh diều
Video AI khởi động Toán 11 cánh diều hấp dẫn
Câu hỏi và bài tập trắc nghiệm toán 11 cánh diều
Đề thi toán 11 cánh diều
File word đáp án toán 11 cánh diều
Bài tập file word Toán 11 Cánh diều
Kiến thức trọng tâm Toán 11 cánh diều
Đề kiểm tra 15 phút Toán 11 cánh diều
Phiếu học tập theo bài Toán 11 cánh diều cả năm
Trắc nghiệm đúng sai Toán 11 cánh diều cả năm
Trắc nghiệm dạng câu trả lời ngắn Toán 11 cánh diều cả năm
