Giáo án powerpoint dạy thêm Toán 11 chân trời Chương 5 Bài 2: Trung vị và tứ phân vị của mẫu số liệu ghép nhóm
Tải giáo án PowerPoint dạy thêm Toán 11 chân trời sáng tạo Chương 5 Bài 2: Trung vị và tứ phân vị của mẫu số liệu ghép nhóm. Giáo án điện tử thiết kế hiện đại, đẹp mắt, nhiều bài tập ôn tập, mở rộng kiến thức phong phú. Tài liệu tải về và chỉnh sửa được. Mời thầy cô và các bạn kéo xuống theo dõi.
Xem: => Giáo án toán 11 chân trời sáng tạo
Click vào ảnh dưới đây để xem 1 phần giáo án rõ nét











Các tài liệu bổ trợ khác
Xem toàn bộ: Giáo án powerpoint dạy thêm toán 11 chân trời sáng tạo đủ cả năm
THÂN MẾN CHÀO ĐÓN CẢ LỚP ĐẾN VỚI TIẾT HỌC HÔM NAY!
KHỞI ĐỘNG
+ Cho mẫu số liệu ghép nhóm
Hãy nêu cách xác định trung vị của mẫu số liệu trên.
BÀI 2:
TRUNG VỊ VÀ TỨ PHÂN VỊ CỦA MẪU SỐ LIỆU GHÉP NHÓM
HỆ THỐNG KIẾN THỨC
- Trung vị
Gọi n là cỡ mẫu, giả sử nhóm [u_m;u_(m+1) ) chứa trung vị;
n_m là tần số của nhóm chứa trung vị, C=n_1+n_2+…+n_(m-1)
M_e=u_m+(n/2-C)/n_m ⋅(u_(m+1)-u_m ),
- Ý nghĩa:
+ Từ dữ liệu ghép nhóm nói chung không thể xác định chính xác trung vị của mẫu số liệu gốc.
+ Trung vị của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho mẫu số liệu gốc và có thể lấy làm giá trị đại diện cho mẫu số liệu.
- Tứ phân vị
- Giả sử nhóm [u_m;u_(m+1) ) chứa tứ phân vị thứ nhất;
n_m là tần số của nhóm chứa tứ phân vị thứ nhất , C=n_1+n_2+…+n_(m-1)
Q_1=u_m+(n/4-C)/n_m ⋅(u_(m+1)-u_m ).
trong đó, n là cỡ mẫu, m_ρ là tần số nhóm p, với p=1 ta quy ước m_1+…+m_(p-1)=0.
- Giả sử nhóm [u_j;u_(j+1) ) chứa tứ phân vị thứ ba;
n_j là tần số của nhóm chứa tứ phân vị thứ ba, C=n_1+n_2+…+n_(j-1)
Q_3=u_j+(3n/4-C)/n_j ⋅(u_(j+1)-u_j )". "
- Chú ý: Nếu tứ phân vị thứ k là 1/2 (x_m+x_(m+1) ), trong đó x_m và x_(m+1) thuộc hai nhóm liên tiếp, ví dụ x_m∈[u_(j-1);u_j) và x_(m+1)∈[u_j;u_(j+1)) thì ta lấy Q_k=u_j.
- Tứ phân vị thứ hai Q_2 chính là trung vị M_e.
- Ý nghĩa:
+ Ba điểm tứ phân vị chia mẫu số liệu đã sắp xếp theo thứ tự không giảm thành bốn phần đều nhau.
+ Tứ phân vị thứ nhất và thứ ba đo xu thế trung tâm của nửa dưới ( các dữ liệu nhỏ hơn Q_2) và nửa trên (các dữ liệu lớn hơn Q_2) của mẫu số liệu.
LUYỆN TẬP, VẬN DỤNG
PHIẾU BÀI TẬP
DẠNG 1: Tính trung vị của mẫu số liệu
Bài 1. Một trường trung học phổ thông đo chiều cao cho học sinh nam của lớp 11(đơn vị: centimét):
■(160&161&161&162&162&162&163&163&163&164&164&164&164@165&165&165&165&165&166&166&166&166&167&167&168&168@168&168&169&169&170&171&171&172&172&174&&&)Hãy lập bảng tần số ghép nhóm với năm nhóm có độ dài bằng nhau.
Trung vị của mẫu số liệu là bao nhiêu?
Giải
|
Chiều cao |
[160;163) |
[163;166) |
[166;169) |
[169;172) |
[172;175) |
|
Số học sinh |
6 |
12 |
10 |
5 |
3 |
Gọi x_1;x_2;…;x_36 là chiều cao của 36 học sinh xếp theo thứ tự không giảm.
Trung vị của dãy số liệu là 1/2(x_18+x_19). Do x_18∈[163;166) và x_19∈[166;169) nên trung vị của mẫu số liệu ghép nhóm là M_e=166.
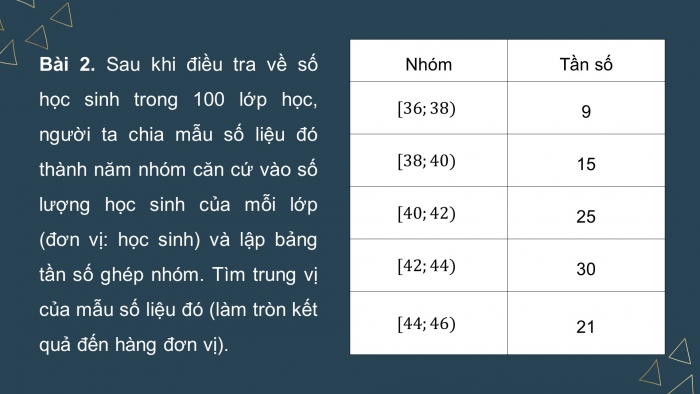
Bài 2. Sau khi điều tra về số học sinh trong 100 lớp học, người ta chia mẫu số liệu đó thành năm nhóm căn cứ vào số lượng học sinh của mỗi lớp (đơn vị: học sinh) và lập bảng tần số ghép nhóm. Tìm trung vị của mẫu số liệu đó (làm tròn kết quả đến hàng đơn vị).
|
Nhóm |
Tần số |
|
[36;38) |
9 |
|
[38;40) |
15 |
|
[40;42) |
25 |
|
[42;44) |
30 |
|
[44;46) |
21 |
Giải
Cỡ mẫu là n=100. Ta có n/2=100/2=50.
Gọi x_1;x_2;…;x_100 là số học sinh của 100 lớp học, giả sử xếp theo thứ tự không giảm.
Nhóm chứa trung vị là: [42;44)
có p=4, a_4=42;m_4=30;m_1+m_2+m_3=9+15+25=49;a_5-a_4=2
Áp dụng công thực, ta có trung vị của mẫu số liệu là:
M_e=42+((50-49)/30)⋅2≈42" (học sinh). "
Bài 3. Số cuộc gọi điện thoại một người thực hiện mỗi ngày trong 30 ngày được lựa chọn ngẫu nhiên được thống kê trong bảng sau:
|
Số cuộc gọi |
[2,5;5,5) |
[5,5;8,5) |
[8,5;11,5) |
[11,5;14,5) |
[14,5;17,5) |
|
Số ngày |
5 |
13 |
7 |
3 |
2 |
Hãy tìm trung vị của mẫu số liệu.
Giải
Cỡ mẫu n = 30
Gọi x_1;x_2;…;x_30 là số cuộc gọi điện thoại được thực hiện xếp theo thứ tự không giảm.
Tứ phân vị thứ hai của dãy số liệu là 〖1/2(x〗_15+x_16)∈[5,5;8,5). Do đó tứ phân vị thứ hai của mẫu số liệu ghép nhóm là
Q_2=M_e=5,5+(30/2-5)/13⋅3≈7,8.
Bài 4. Thời gian (phút) truy cập Internet mỗi buổi tối của một học sinh được cho trong bảng sau:
|
Thời gian (phút) |
[9,5;12,5) |
[12,5;15,5) |
[15,5;18,5) |
[18,5;21,5) |
[21,5;24,5) |
|
Số học sinh |
3 |
12 |
15 |
24 |
2 |
Tính trung vị của mẫu số liệu ghép nhóm này.
Giải
Cỡ mẫu: n = 3 + 12 + 15 + 24 + 2 = 56.
Gọi x_1;x_2;…;x_56 là thời gian vào Internet của 56 học sinh xếp theo thứ tự không giảm.
Khi đó trung vị là 1/2 (x_28+x_29 )∈[15,5;18,5).
Ta xác định được n=56,n_m=15,C=15,u_m=15,5,u_(m+1)=28,5.
Trung vị của mẫu số liệu ghép nhóm là
M_e=15,5+(56/2-15)/15⋅(18,5-15,5)=18,1." "
PHIẾU BÀI TẬP
DẠNG 2: Tính tứ phân vị thứ nhất và thứ ba của mẫu số liệu
...
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Giáo án powerpoint dạy thêm toán 11 chân trời sáng tạo đủ cả năm
ĐẦY ĐỦ GIÁO ÁN CÁC BỘ SÁCH KHÁC
GIÁO ÁN WORD LỚP 11 CHÂN TRỜI SÁNG TẠO
GIÁO ÁN POWERPOINT LỚP 11 CHÂN TRỜI SÁNG TẠO
GIÁO ÁN CHUYÊN ĐỀ 11 CHÂN TRỜI SÁNG TẠO
GIÁO ÁN DẠY THÊM 11 CHÂN TRỜI SÁNG TẠO
CÁCH ĐẶT MUA:
Liên hệ Zalo: Fidutech - nhấn vào đây
