Giáo án PPT dạy thêm Toán 12 cánh diều Bài tập cuối chương II

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC

HÔM NAY!

KHỞI ĐỘNG

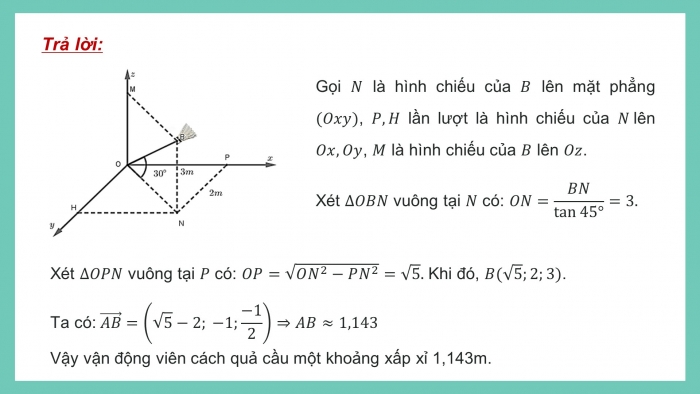
Một vận động viên cầu lông đang thi đấu trên sân. Vận động viên đang nhảy lên vị trí và đập cầu tại vị trí . Tính khoảng cách của vận động và cầu lông

và cách mặt phẳng .

Gọi là hình chiếu của lên mặt phẳng , lần lượt là hình chiếu của lên , là hình chiếu của lên .

Xét vuông tại có: Khi đó, .

Vậy vận động viên cách quả cầu một khoảng xấp xỉ 1,143m.

CHƯƠNG II. TOẠ ĐỘ CỦA VECTƠ TRONG KHÔNG GIAN

BÀI TẬP CUỐI CHƯƠNG II

Giải:

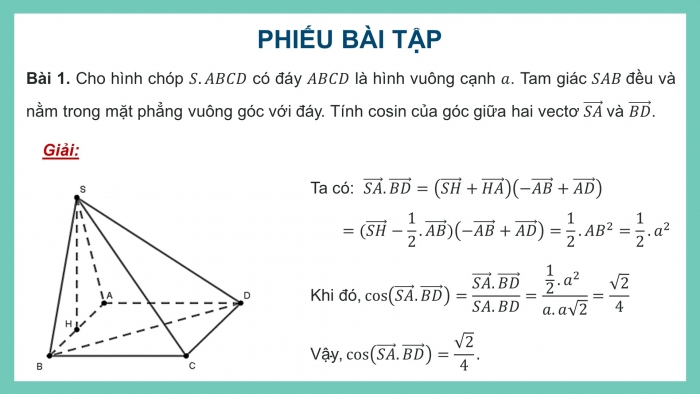
Bài 1. Cho hình chóp có đáy là hình vuông cạnh . Tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính cosin của góc giữa hai vectơ và .

PHIẾU BÀI TẬP

Ta có:  

Bài 2. Trong không gian , cho hình lăng trụ tam giác có

.

a) Tìm tọa độ vectơ  b) Tìm tọa độ vectơ của các điểm .

Giải:

a) Ta có: .

b) Gọi . Ta có:

Vì là hình bình hành nên

Khi đó:

Thực hiện tương tự, ta được .

Vậy .

Bài 3. Tìm tọa độ của các vectơ biết rằng:

a) ; b) ; c) .

Giải:

a) Vì

Vậy

b) Vì .

Vậy .

c) Vì .

Vậy .

Giải:

Bài 4. Cho hình lăng trụ đứng có đáy là tam giác vuông cân tại . Gọi là trung điểm là trung điểm . Chọn hệ trục tọa độ có gốc tọa độ ; các điểm lần lượt nằm trên các tia . Tính tọa độ các vectơ và 

Ta có:

Vì là trung điểm của nên

Khi đó

Ta có:

Giải:

Bài 4. Cho hình lăng trụ đứng có đáy là tam giác vuông cân tại . Gọi là trung điểm là trung điểm . Chọn hệ trục tọa độ có gốc tọa độ ; các điểm lần lượt nằm trên các tia . Tính tọa độ các vectơ và 

Áp dụng quy tắc hình bình hành

Vì là trung điểm của nên

Khi đó 

Vậy .

Bài 5. Cho tứ diện có Gọi là trọng tâm của tam giác là trọng tâm của tứ diện. Tìm tọa độ điểm .

Vì là trọng tâm của tam giác nên .

Gọi .

Ta có:  ;

; ;

Do là tâm của tứ diện nên 

Giải:

Bài 5. Cho tứ diện có Gọi là trọng tâm của tam giác là trọng tâm của tứ diện. Tìm tọa độ điểm .

Giải:

Giải:

Ta có:  

Vì là hình bình hành nên  

Gọi

Ta có:  

.

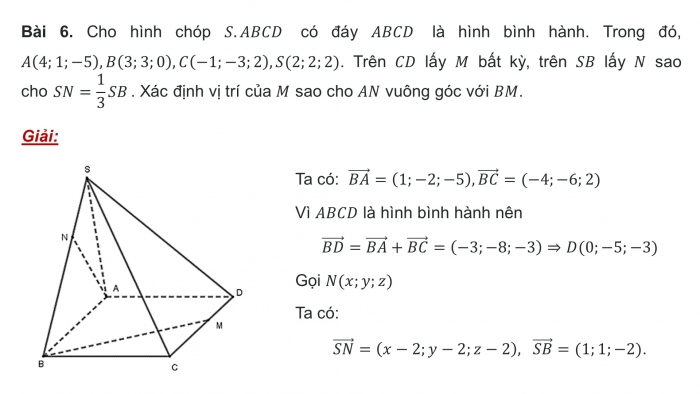
Bài 6. Cho hình chóp có đáy là hình bình hành. Trong đó, . Trên lấy bất kỳ, trên lấy sao cho   . Xác định vị trí của sao cho vuông góc với .

Giải:

Gọi .

Ta có:  

Giả sử:  

.

Giải:

Bài 7. Trong không gian . Cho hình lăng trụ tam giác có . Tính thể tích khối lăng trụ.

Giải:

Ta có:  ;

Khi đó

Vậy .

TRẮC NGHIỆM

Câu 1. Cho tứ tam giác . Gọi là trọng tâm tam giác . Khẳng định nào sau đây là đúng?

C

A

D

B

A

Phần 1: Câu trắc nghiệm nhiều phương án lựa chọn

Câu 2. Cho hình lăng trụ . Gọi lần lượt là trung điểm . Khẳng định nào sau đây là sai?

C

A

D

B

C

Câu 3. Trong không gian với hệ tọa độ , cho , . Khi đó, bằng

C

A

D

B

A

Câu 4. Trong không gian với hệ tọa độ , cho , . Tích vô hướng  bằng

--------------- Còn tiếp ---------------