Giáo án powerpoint dạy thêm Toán 11 kết nối Bài tập cuối chương 6
Tải giáo án Powerpoint dạy thêm Toán 11 kết nối tri thức Bài tập cuối chương 6. Giáo án điện tử thiết kế hiện đại, đẹp mắt, nhiều bài tập ôn tập, mở rộng kiến thức phong phú. Tài liệu tài về và chỉnh sửa được. Mời thầy cô và các bạn kéo xuống theo dõi.
Xem: => Giáo án toán 11 kết nối tri thức
Click vào ảnh dưới đây để xem 1 phần giáo án rõ nét





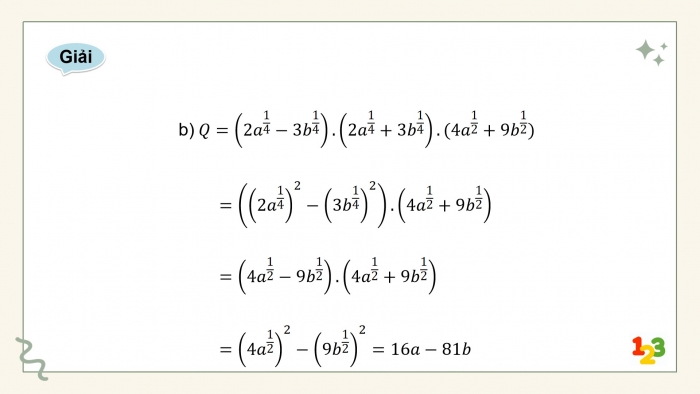





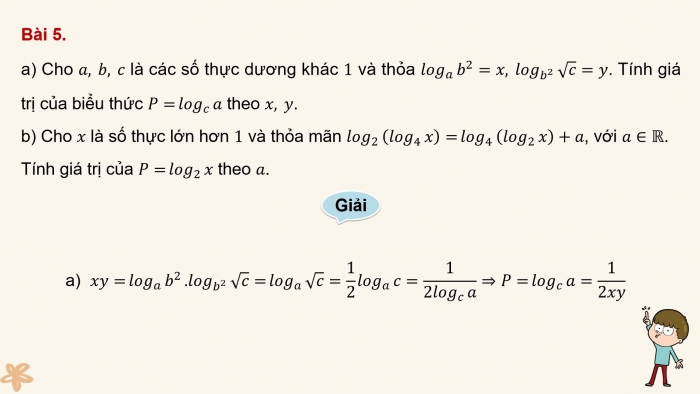
Các tài liệu bổ trợ khác
Xem toàn bộ: Giáo án powerpoint dạy thêm toán 11 kết nối tri thức đủ cả năm
CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC HÔM NAY!
CHƯƠNG VI. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
BÀI TẬP CUỐI CHƯƠNG VI
PHIẾU BÀI TẬP SỐ 1
Bài 1. Cho các số thực dương a và b. Biểu thức thu gọn của biểu thức
P=(2a^1/4−3b^1/4)⋅(2a^1/4+3b^1/4)⋅(4a^1/2+9b^1/2) có dạng là P=xa+yb. Tính x+y?
Giải
Ta có: P=(2a^1/4−3b^1/4)⋅(2a^1/4+3b^1/4)⋅(4a^1/2+9b^1/2)=((2a^1/4)^2−(3b^1/4)^2)⋅(4a^1/2+9b^1/2)
=(4a^1/2−9b^1/2)⋅(4a^1/2+9b^1/2)=(4a^1/2)^2−(9b^1/2)^2=16a−81b
Do đó: x=16;y=−81.
Bài 2. Thu gọn các biển thức sau:
- a) P=(a^1/2+2/a+2a^1/2+1−a^1/2−2/a−1).(a^1/2+1)/a^1/2, (a>0,a≠±1)
- b) Q=(2a^1/4−3b^1/4).(2a^1/4+3b^1/4).(4a^1/2+9b^1/2), (a>0,b>0)
- c) T=2(a+b)^−1.(ab)^1/2.[1+1/4(√a/b−√b/a)^2]^1/2, (a>0,b>0)
Giải
- a) P=(a^1/2+2/a+2a^1/2+1−a^1/2−2/a−1).(a^1/2+1)/a^1/2
=(√a+2/(√a+1)^2−√a−2/(√a−1)(√a+1)).√a+1/√a=(√a+2/√a+1−√a−2/√a−1).1/√a
=2√a/a−1.1/√a=2/a−1
- b) Q=(2a^1/4−3b^1/4).(2a^1/4+3b^1/4).(4a^1/2+9b^1/2)
=((2a^1/4)^2−(3b^1/4)^2).(4a^1/2+9b^1/2)
=(4a^1/2−9b^1/2).(4a^1/2+9b^1/2)
=(4a^1/2)^2−(9b^1/2)^2=16a−81b
- c) T=2(a+b)^−1.(ab)^1/2.[1+1/4(√a/b−√b/a)^2]^1/2
=2(a+b)^−1.(ab)^1/2.[1+1/4(a−b/√ab)^2]^1/2=2(a+b)^−1.(ab)^1/2.[1+(a−b)^2/4ab]^1/2
=2(a+b)^−1.(ab)^1/2.[(a+b)^2/4ab]^1/2=21/a+b.(ab)^1/2.(a+b)/2(ab)^1/2=1
Bài 3. Tính giá trị các biểu thức sau:
- a) 8^−3.(1/16)^−3:4^−2; b) 125^2/3.27^2/3; c)(1/8)^−2/3+0,16^3/2; d) (32)^−0,2−(1/64)^−1/6+(8/27)^1/3
Giải
- a) 8^−3.(1/16)^−3:4^−2=1/8^3 . 1/(1/16)^3 :1/4^2=1/8^3.1/1/4096.16=1/512.4096 . 16=128
- b) 125^2/3 . 27^2/3=(125/27)^2/3=(√(3&125/27))^2=(5/3)^2=25/9
- c) (1/8)^−2/3+0,16^3/2=8^2/3+(16/100)^2/3=√(3&8^2)+(√16/100)^3=4:(4/10)^3=508/125
- d) (32)^−0,2−(1/64)^−1/6+(8/27)^1/3=(32)^−1/5−1/(1/64)^1/6+ (8/27)^1/3=1/√(5&32)−1/√(6&1/64)+√(3&8/27)
=1/2−1/1/2+2/3=1/2−2+2/3=−5/6
Bài 4. a) Biết a=log_25,b=log_53. Khi đó tính giá trị của log_2415 theo a.
- b) Cho log_1227=a. Khi đó tính giá trị của log_616 được theo a.
- c) Cho a=log_23;b=log_35;c=log_72. Khi đó tính giá trị của biểu thức log_14063 theo a,b,c.
- d) Đặt a=log_315;b=log_310. Hãy biểu diễn log_√350 theo a và b.
Giải
- a) log_2415=log_215/log_224=log_23.5/log_23.2^3=log_23+log_25/log_23+3
=log_23+log_23⋅log_35/log_23+3=a+a⋅1/b/3+a=a+ab/ab+3b
- b) a=log_1227=log_227/log_212=3log_23/2+log_23⇒log_23=2a/3−a⇒log_616=4(3−a)/3+a
- c) log_14063=log_263/log_2140=log_23^2⋅7/log_22^2⋅5.7=2log_23+log_27/2+log_25+log_27
=2log_23+1/log_72/2+log_23⋅log_35+log_72=2a+1/c/2+ab+1/c=1+2ac/1+2c+abc
- d) log_√350=log_3^1/250=2log_350=2log_3(10.5)=2(log_310+log_35)
=2(log_310+log_315−log_33)=2(a+b−1)
Bài 5.
- a) Cho a, b, c là các số thực dương khác 1 và thỏa log_ab^2=x, log_b^2√c=y. Tính giá trị của biểu thức P=log_ca theo x, y.
- b) Cho x là số thực lớn hơn 1 và thỏa mãn log_2(log_4x)=log_4(log_2x)+a, với a∈ℝ.
Tính giá trị của P=log_2x theo a.
Giải
- a) xy=log_ab^2.log_b^2√c=log_a√c=1/2log_ac=1/2log_ca⇒P=log_ca=1/2xy
- b) log_2(log_4x)=log_4(log_2x)+a⇔log_2(log_2x/2)=1/2log_2(log_2x)+a
⇔log_2(log_2x)−1=1/2log_2(log_2x)+a⇔log_2(log_2x)=2a+2
⇔log_2x=2^2a+2⇔log_2x=4^a+1
Bài 6. Biết rằng năm 2001, dân số Việt Nam là 78685800 người và tỉ lệ tăng dân số năm đó là 1,7%. Cho biết sự tăng dân số được ước tính theo công thức S=A.e^N.r (trong đó A: là dân số của năm lấy làm mốc tính, S là dân số sau N năm, r là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu người?
Giải
Ta có S=A.e^N.r⇒N=1/r.lnS/A
Để dân số nước ta ở mức 120 triệu người thì cần số năm N=100/1,7.ln120.10^6/78685800≈25
Lúc đấy là năm 2001+25=2026.
Bài 7. Chứng minh rằng: a) Nếu 4a^2+9b^2=4ab thìlg2a+3b/4=lga+lgb/2
Giải
Ta có: 4a^2+9b^2=4ab ⟺4a^2+12ab+9b^2=16ab⟺(2a+3b)^2=16ab
⟺(2a+3b/4)^2=ab
Từ đó suy ra: lg(2a+3b/4)^2=lg(ab)⇔2lg(2a+3b/4)=lga+lgb
⇔lg(2a+3b/4)=(lga+lgb)/2
- b) Nếu a=10^1/1−lgb;b=10^1/1−lgc thì c=10^1/1−lga
Giải
Ta có: a=10^1/1−lgb⇔lga=lg10^1/1−lgb=1/1−lgb
Suy ralgb=1−1/lga=lga−1/lga (1)
Tương tự: b=10^1/1−lgc⇔lgb=lg10^1/1−lgc=1/1−lgc (2)
Từ (1) và (2) ta có: lga−1/lga =1/1−lgc⇔lgc=1−lga/1−lga=1/1−lga
⇒10^lgc=10^1/1−lga⇔c=10^1/1−lga
- c) Nếu a^2+b^2=7ab thì log_7a+b/3=1/2(log_7a+log_7b)
Giải
Ta có: a^2+b^2=7ab⇔ a^2+b^2+2ab=9ab⇔(a+b)^2=9ab
⇔a+b=3√ab⇔a+b/3=√ab
Suy ra:log_7a+b/3=log_7√ab⇔log_7a+b/3=log_7ab^1/2
⇔log_7a+b/3=1/2(log_7a+log_7b)
PHIẾU BÀI TẬP SỐ 2
Bài 1. Tìm tập xác định D của hàm số
- a) y=ln(1−log_2x); b) y=log_1/x(1−2x+x^2); c) y=e^x/e^x−1
...
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Giáo án powerpoint dạy thêm toán 11 kết nối tri thức đủ cả năm
ĐẦY ĐỦ GIÁO ÁN CÁC BỘ SÁCH KHÁC
GIÁO ÁN WORD LỚP 11 KẾT NỐI TRI THỨC
GIÁO ÁN POWERPOINT LỚP 11 KẾT NỐI TRI THỨC
GIÁO ÁN CHUYÊN ĐỀ LỚP 11 KẾT NỐI TRI THỨC
GIÁO ÁN DẠY THÊM 11 KẾT NỐI TRI THỨC
CÁCH ĐẶT MUA:
Liên hệ Zalo: Fidutech - nhấn vào đây
