Giáo án powerpoint dạy thêm Toán 11 kết nối Bài tập cuối chương 7

CHÀO MỪNG CÁC EM 

ĐÃ ĐẾN VỚI TIẾT HỌC! 

CHƯƠNG VII. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN 

BÀI TẬP CUỐI CHƯƠNG VII 

PHIẾU BÀI TẬP SỐ 1 

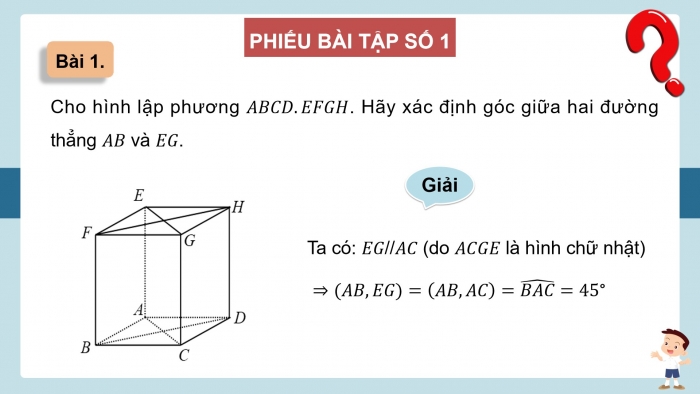
Bài 1. 

Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa hai đường thẳng AB và EG. 

Giải 

Ta có: EG//AC (do ACGE là hình chữ nhật) 

⇒(AB,EG)=(AB,AC)=(BAC) ̂=45° 

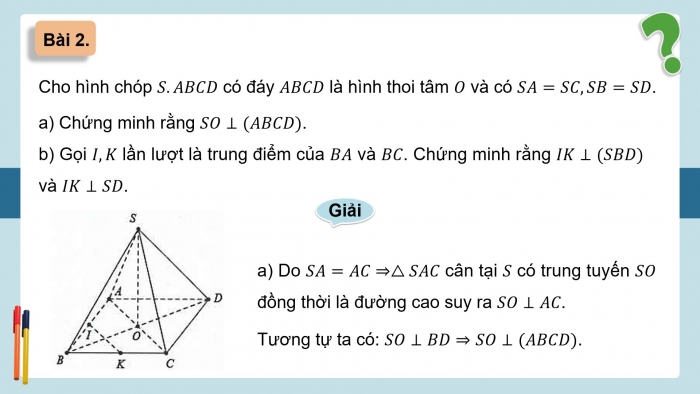
Bài 2. 

Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và có SA=SC,SB=SD. 

1. a) Chứng minh rằng SO⊥(ABCD).
2. b) Gọi I,K lần lượt là trung điểm của BA và BC. Chứng minh rằng IK⊥(SBD) và IK⊥SD.

Giải 

1. a) Do SA=AC⇒△SAC cân tại S có trung tuyến SO đồng thời là đường cao suy ra SO⊥AC.

Tương tự ta có: SO⊥BD⇒SO⊥(ABCD). 

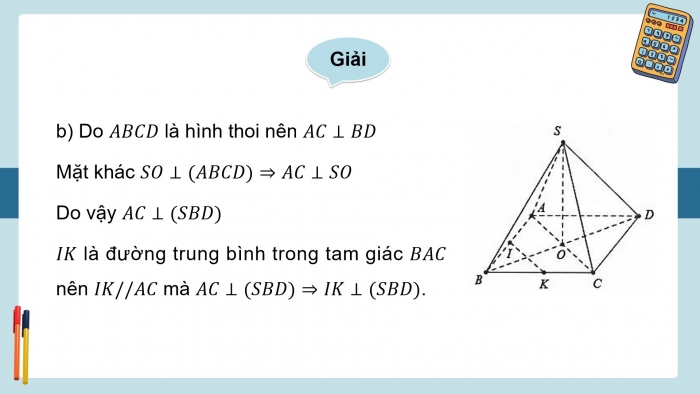
1. b) Do ABCD là hình thoi nên AC⊥BD

Mặt khác SO⊥(ABCD)⇒AC⊥SO 

Do vậy AC⊥(SBD) 

IK là đường trung bình trong tam giác BAC nên IK//AC mà AC⊥(SBD)⇒IK⊥(SBD). 

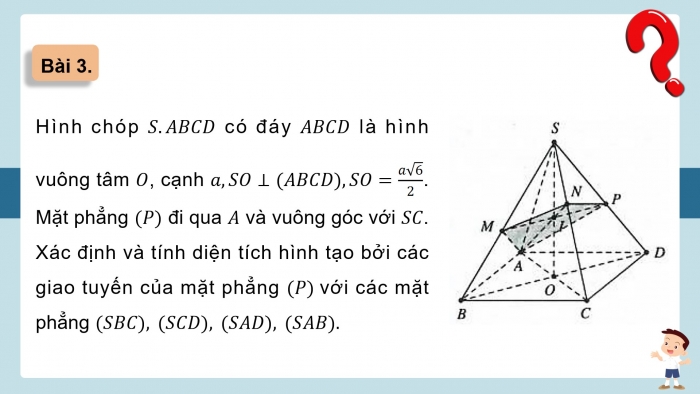
Bài 3. 

Hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a,SO⊥(ABCD),SO=a√6/2. Mặt phẳng (P) đi qua A và vuông góc với SC. Xác định và tính diện tích hình tạo bởi các giao tuyến của mặt phẳng (P) với các mặt phẳng (SBC), (SCD), (SAD), (SAB). 

Giải 

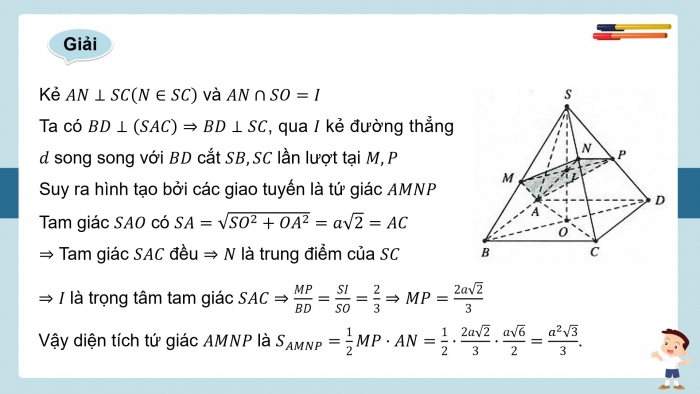
Kẻ AN⊥SC(N∈SC) và AN∩SO=I 

Ta có BD⊥(SAC)⇒BD⊥SC, qua I kẻ đường thẳng d song song với BD cắt SB,SC lần lượt tại M,P 

Suy ra hình tạo bởi các giao tuyến là tứ giác AMNP 

Tam giác SAO có SA=√SO^2+OA^2=a√2=AC 

⇒ Tam giác SAC đều ⇒N là trung điểm của SC 

⇒I là trọng tâm tam giác SAC ⇒MP/BD=SI/SO=2/3⇒MP=2a√2/3 

Vậy diện tích tứ giác AMNP là S_AMNP=1/2MP⋅AN=1/2⋅2a√2/3⋅a√6/2=a^2√3/3. 

Bài 4. 

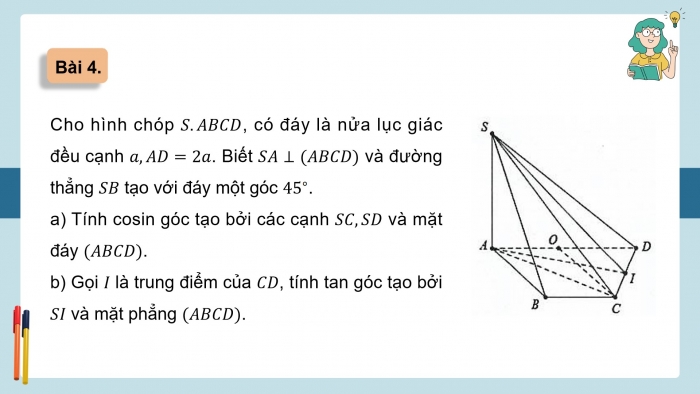
Cho hình chóp S.ABCD, có đáy là nửa lục giác đều cạnh a,AD=2a. Biết SA⊥(ABCD) và đường thẳng SB tạo với đáy một góc 45^∘. 

1. a) Tính cosin góc tạo bởi các cạnh SC,SD và mặt đáy (ABCD).
2. b) Gọi I là trung điểm của CD, tính tan góc tạo bởi SI và mặt phẳng (ABCD).

Giải 

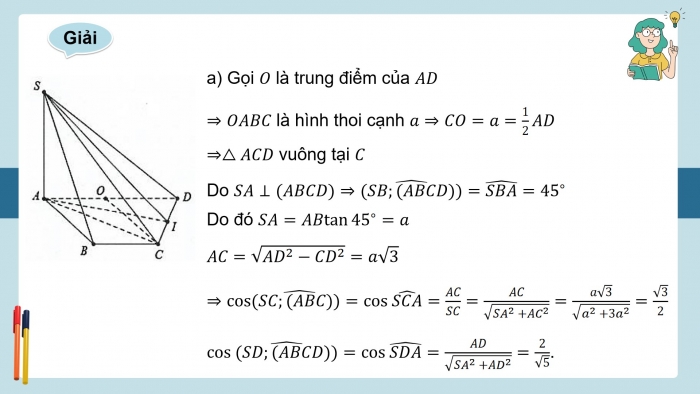
1. a) Gọi O là trung điểm của AD

⇒OABC là hình thoi cạnh a⇒CO=a=1/2AD 

⇒△ACD vuông tại C 

Do SA⊥(ABCD)⇒((SB;(ABCD))) ̂=(SBA) ̂=45^∘ 

Do đó SA=ABtan45^∘=a 

AC=√AD^2−CD^2=a√3 

⇒cos⁡((SC;(ABC))) ̂=cos⁡(SCA) ̂=AC/SC=AC/√SA^2+AC^2=a√3/√a^2+3a^2=√3/2   

cos⁡((SD;(ABCD))) ̂=cos⁡(SDA) ̂=AD/√SA^2+AD^2=2/√5. 

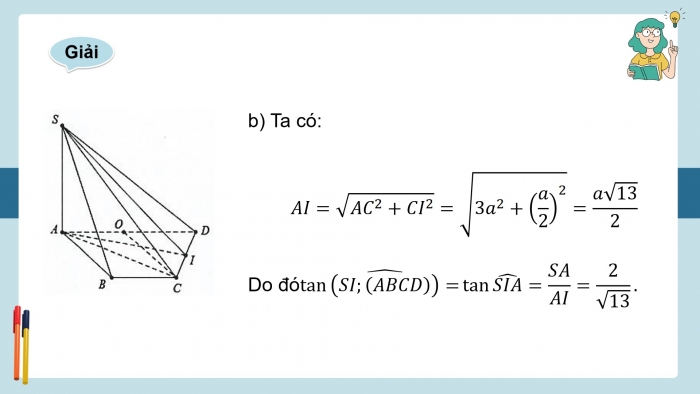
1. b) Ta có:

AI=√AC^2+CI^2=√3a^2+(a/2)^2=a√13/2 

Do đótan((SI;(ABCD))) ̂=tan(SIA) ̂=SA/AI=2/√13. 

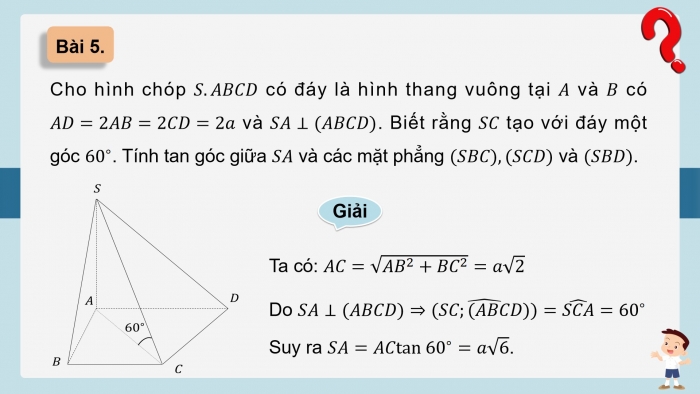
Bài 5. 

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B có           AD=2AB=2CD=2a và SA⊥(ABCD). Biết rằng SC tạo với đáy một góc 60^∘. Tính tan góc giữa SA và các mặt phẳng (SBC),(SCD) và (SBD). 

Giải 

Ta có: AC=√AB^2+BC^2=a√2 

Do SA⊥(ABCD)⇒((SC;(ABCD))) ̂=(SCA) ̂=60^∘ 

Suy ra SA=ACtan⁡60^∘=a√6. 

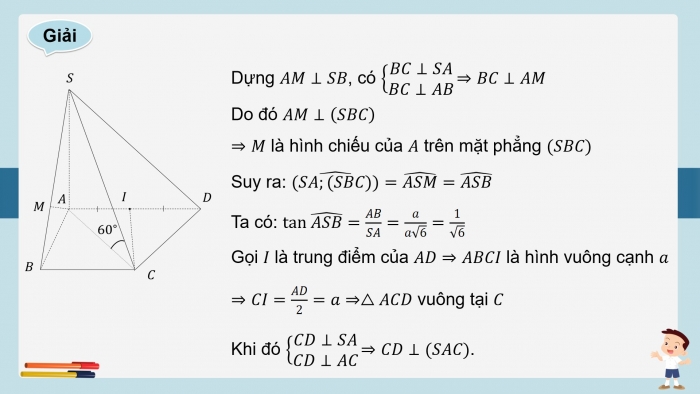
Dựng AM⊥SB, có {■(BC⊥SA@BC⊥AB)⇒BC⊥AM┤ 

Do đó AM⊥(SBC) 

⇒M là hình chiếu của A trên mặt phẳng (SBC) 

Suy ra: ((SA;(SBC))) ̂=(ASM) ̂=(ASB) ̂ 

Ta có: tan⁡(ASB) ̂=AB/SA=a/a√6=1/√6 

Gọi I là trung điểm của AD⇒ABCI là hình vuông cạnh a 

⇒CI=AD/2=a⇒△ACD vuông tại C 

Khi đó {■(CD⊥SA@CD⊥AC)⇒CD⊥(SAC)┤. 

Dựng AN⊥SC⇒((SA;(SCD))) ̂=(ASN) ̂=(ASC) ̂ 

Ta có: tan⁡(ASC) ̂=AC/SA=a√2/a√6=1/√3 

Dựng {■(AE⊥BD@AF⊥SE)⇒((SA;(SBD))) ̂=(ASF) ̂=(ASE) ̂┤ 

Mặt khác AE=AB⋅AD/√AB^2+AD^2=2a/√5 

⇒tan⁡(ASE) ̂=AE/SA=√30/15. 

PHIẾU BÀI TẬP SỐ 2 

Bài 1. 

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA⊥(ABCD), SA=x. Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60^o. 

Giải 

* Trong (SAB) dựng AI⊥SB ta chứng minh được AI⊥(SBC) (1) 

Trong (SAD) dựng AJ⊥SD ta chứng minh được AJ⊥(SCD) (2) 

Từ (1) và (2)  góc ((SBC),(SCD))=(AI,AJ)=(IAJ) ̂ 

* Ta chứng minh được AI=AJ 

Do đó, nếu góc (IAJ) ̂=60^o thì ΔAIJ đều  

AI=AJ=IJ 

ΔSAB vuông tại A có AI là đường cao  

AI.SB=SA.AB AI=SA.AB/SB (3) 

Và có SA^2=SI.SB SI=SA^2/SB (4) 

Ta chứng minh được IJ//BD  

 IJ/BD=SI/SB IJ=SI.BD/SB =SA^2.BD/SB^2  (5) 

Thế (3) và (5) vào AI=IJ AB=SA.BD/SB  

 AB.SB=SA.BD  

 a.√x^2+a^2=x.a√2  

 x^2+a^2=2x^2 x=a 

Bài 2. 

Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA⊥(ABCD). 

1. a) Chứng minh (SAC)⊥(SBD).
2. b) Chứng minh (SAD)⊥(SCD).
3. c) Gọi BE và DF là đường cao trong tam giác SBD. Chứng minh rằng (ACF)⊥(SBC);(AEF)⊥(SAC).

...