Giáo án powerpoint dạy thêm Toán 11 kết nối Bài 25: Hai mặt phẳng vuông góc

CHÀO MỪNG CÁC EM ĐÃ ĐẾN VỚI TIẾT HỌC  

NGÀY HÔM NAY! 

KHỞI ĐỘNG 

Thế nào là góc giữa hai mặt phẳng (P) và (Q)? 

CHƯƠNG VII: QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN 

BÀI 25: HAI MẶT PHẲNG VUÔNG GÓC 

HỆ THỐNG  

KIẾN THỨC 

1. Góc giữa hai mặt phẳng, hai mặt phẳng vuông góc

Cho hai mặt phẳng (P) và (Q). Lấy các đường thẳng a,b tương ứng vuông góc với (P),(Q). Khi đó, góc giữa và b không phụ thuộc vào vị trí của a,b và được gọi là góc giữa hai măt phăng (P) và (Q). 

Hai mặt phẳng (P) và (Q) được gọi là vuông góc với nhau nếu góc giữa chúng bằng 90^∘. 

Chú ý: Nếu φ là góc giữa hai mặt phẳng (P) và (Q) thì 0≤φ≤90^o. 

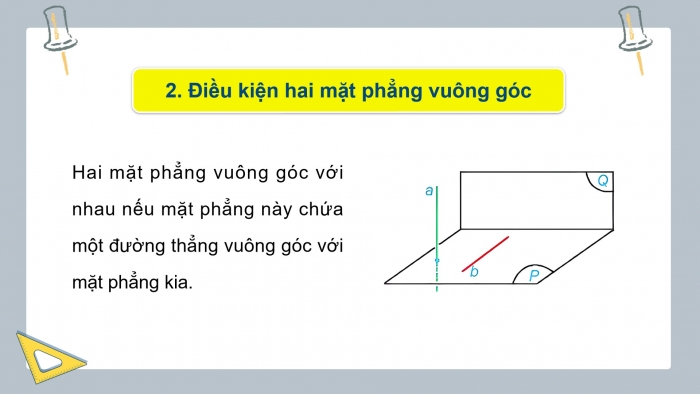
2. Điều kiện hai mặt phẳng vuông góc

Hai mặt phẳng vuông góc với nhau nếu mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia. 

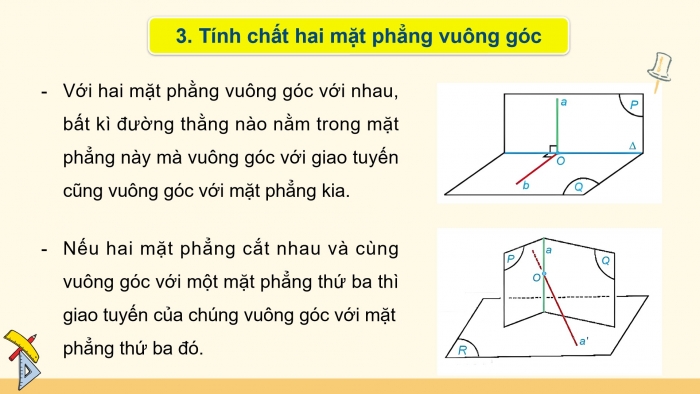
3. Tính chất hai mặt phẳng vuông góc

Với hai mặt phằng vuông góc với nhau, bất kì đường thằng nào nằm trong mặt phẳng này mà vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia. 

Nếu hai mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó. 

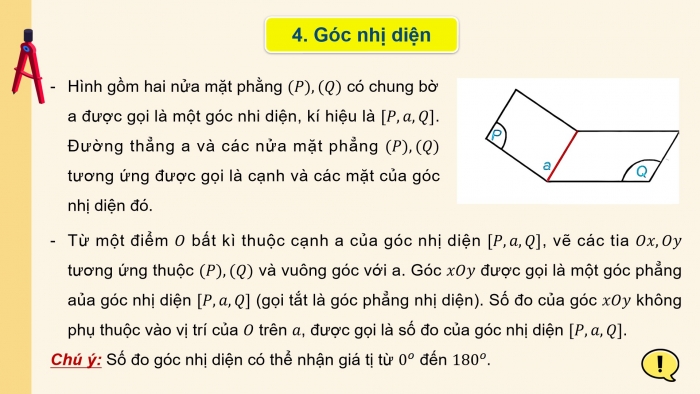
4. Góc nhị diện

Hình gồm hai nửa mặt phằng (P),(Q) có chung bờ a được gọi là một góc nhi diện, kí hiệu là [P,a,Q]. Đường thẳng a và các nửa mặt phẳng (P),(Q) tương ứng được gọi là cạnh và các mặt của góc nhị diện đó. 

Từ một điểm O bất kì thuộc cạnh a của góc nhị diện [P,a,Q], vẽ các tia Ox,Oy tương ứng thuộc (P),(Q) và vuông góc với a. Góc xOy được gọi là một góc phẳng aủa góc nhị diện [P,a,Q] (gọi tắt là góc phẳng nhị diện). Số đo của góc xOy không phụ thuộc vào vị trí của O trên a, được gọi là số đo của góc nhị diện [P,a,Q]. 

Chú ý: Số đo góc nhị diện có thể nhận giá tị từ 0^o đến 180^o. 

5. Một số hình lăng trụ đặc biệt
6. a) Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với mặt đáy.

    Hình lăng trụ đứng có các mặt bên là các hình chữ nhật và vuông góc với mặt đáy. 

1. b) Hình lăng trụ đều là hình lăng trụ đựng có đáy là đa giác đều.

    Hình lăng trụ đều có các mặt bên là các hình chữ nhật có cùng kích thước. 

1. c) Hình hộp đứng là hình lăng trụ đứng, có đáy là hình bình hành.

    Hình hộp đứng có các mặt bên là các hình chữ nhật. 

1. d) Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.

    Hình hộp chữ nhật có các mặt bên là hình chữ nhật. Các đường chéo của hình hộp chữ nhật có độ dài bằng nhau và chúng cắt nhau tại trung điểm của mỗi đường. 

1. e) Hình lập phương là hình hộp chữ nhật có tất cả các cạnh bằng nhau.

    Hình lập phương có các mặt là các hình vuông. 

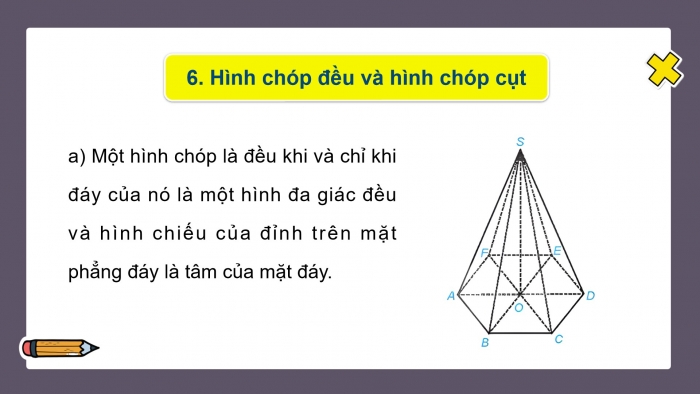
6. Hình chóp đều và hình chóp cụt
7. a) Một hình chóp là đều khi và chỉ khi đáy của nó là một hình đa giác đều và hình chiếu của đỉnh trên mặt phẳng đáy là tâm của mặt đáy.
8. b) Hình chóp cụt

Hình gồm các đa giác đều A_1A_2…A_n^′B_1B_2…B_n và các hình thang cân A_1A_2B_1B_2, A_2A_3B_3B_2,…,A_nA_1B_1B_n được gọi là một hình chóp cụt đều, kí hiệu là A_1A_2…A_n⋅B_1B_2…B_n. 

Các đa giác A_1A_2…A_n,B_1B_2…B_n được gọi là hai mặt đáy, các hình thang A_1A_2B_2B_1, A_2A_3B_3B_2,…,A_nA_1B_1B_n được gọi là các mặt bên của hình chóp cụt. 

Các đoạn thằng A_1B_1,A_2B_2,…,A_nB_n được gọi là các cạnh bên; các cạnh của mặt đáy được gọi là các cạnh đáy của hình chóp cụt. 

Đoạn thẳng HK nối hai tâm của đáy được gọi là đường cao của hình chóp cụt đều. Độ dài của đường cao được gọi là chiều cao của hình chóp cụt. 

LUYỆN TẬP 

PHIẾU BÀI TẬP SỐ 1 

DẠNG 1: Góc giữa hai mặt phẳng 

Phương pháp giải:  

Cách 1: Dùng định nghĩa: 

Xác định hai đường thẳng a, b tương ứng vuông góc với (P), (Q).  

Khi đó  

((P);(Q))=(a;b) 

Cách 2:   

- Tìm giao tuyến ∆ của hai mặt phẳng 

- Chọn điểm I thích hợp trên ∆, từ I ta dựng 2 đường thẳng, đường thẳng a nằm trên mặt phẳng (P) và vuông góc với ∆ , đường thẳng b nằm trên mặt phẳng (Q) và vuông góc với ∆ 

Khi đó ((P);(Q))=(a;b). 

Cách 2: 

- Tìm giao tuyến ∆ của hai mặt phẳng 

- Chọn điểm M thích hợp nằm trên 1 trong 2 mặt phẳng, từ điểm M dựng hình chiếu vuông góc H đến mặt phẳng còn lại. Dựng hình chiếu vuông góc I của điểm M hoặc điểm H đến giao tuyến ∆ 

Khi đó ((P);(Q))= (MIH) ̂. 

Cách 3: Dùng khoảng cách (nội dung bài sau). 

Cách 4: Sử dụng công thức hình chiếu (Mở rộng) 

Giả sử góc giữa hai mặt phẳng (P) và (Q) bằng φ. Lấy trong mặt phẳng (P) một đa giác (H) có diện tích S, hình chiếu vuông góc của đa giác (H) lên mặt phẳng (Q) là đa giác (H′) có diện tích  S′. Khi đó ta luôn có công thức 

S′=Scosφ. 

Bài 1. Cho tứ diện đều ABCD. Tính côsin góc giữa (ABC) và (ABD). 

Giải: 

Đặt AB=a. Gọi I là trung điểm của AB 

Tam giác ABC đều cạnh a nên CI⊥AB và CI=a√3/2 

Tam giác ABD đều nên DI⊥AB và DI=a√3/2 

Do đó, ((ABC),(ABD))=(CI,DI)=(CID) ̂=α. 

Tam giác CID có 

cosα=IC^2+ID^2−CD^2/2.IC.ID=3a^2/4+3a^2/4−a^2/2.a√3/2.a√3/2=a^2/2/3a^2/2=1/3 

Bài 2. Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc (BAD) ̂=60^0. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và SO=3a/4. Gọi E là trung điểm BC và F là trung điểm BE. Tính góc giữa hai mặt phẳng (SOF) và (SBC). 

Giải: 

ΔBCD đều nên DE⊥BC 

Mặt khác OF//DE⇒BC⊥OF (1) 

Do SO⊥(ABCD)⇒BC⊥SO (2) 

Từ (1) và (2), suy ra BC⊥(SOF) 

⇒(SBC)⊥(SOF) 

Vậy, góc giữa (SOF) và (SBC) bằng 90^o. 

Bài 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Biết SO⊥(ABCD), SO=a√3 và đường tròn ngoại tiếp ABCD có bán kính bằng a. Gọi α là góc hợp bởi mặt bên (SCD) với đáy. Hãy tính giá trị tanα. 

...