Giáo án và PPT Toán 11 kết nối Bài 26: Khoảng cách

BÀI 26. KHOẢNG CÁCH

HOẠT ĐỘNG KHỞI ĐỘNG

- GV yêu cầu HS đọc tình huống mở đầu:

Các đầu phun nước chữa cháy sprinkler cần được lắp đặt theo tiêu chuẩn kĩ thuật, trong đó có tiêu chuẩn về khoảng cách tới từng loại trần, tường, nhà.

- GV đặt câu hỏi gợi mở:

+ Khoảng cách từ đầu phun nước chữa cháy đến mặt đất có thể tính như thế nào?

+ Khoảng cách từ trần nhà đến mặt đất được tính như thế nào?

HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC

Hoạt động 1. Khoảng cách từ một điểm đến một đường thẳng, từ một điểm đến một mặt phẳng

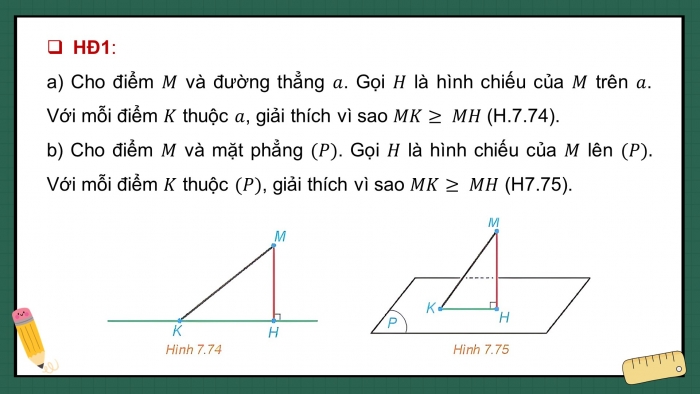
- GV yêu cầu HS thảo luận hoàn thành HĐ 1.

- GV đặt câu hỏi: 

+ Em hãy trình bày định nghĩa khoảng cách từ một điểm đến đường thẳng, mặt phẳng,

+ Nếu thì điểm M và đường thẳng có vị trí như thế nào? Tương tự với Và ngược lại.

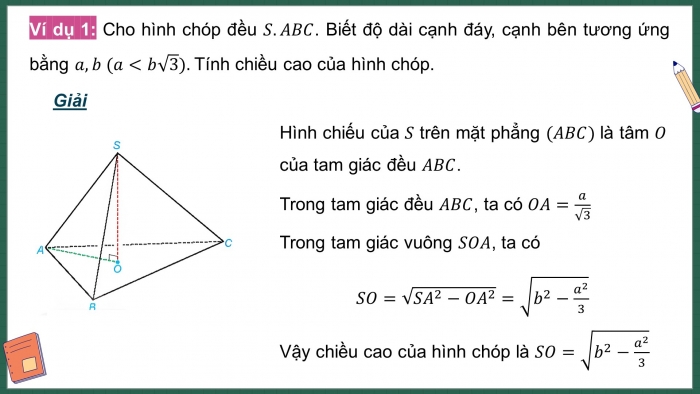
- HS đọc, trình bày Ví dụ 1.

+ Xác định được đoạn thẳng SO là chiều cao của hình chóp.

+ Tính SO dựa vào các định lí hình học.

- HS thực hiện Luyện tập 1.

+ Làm thế nào để xác định hình chiếu của A lên mặt phẳng (BCC”B’)?

Sản phẩm dự kiến:

HĐ 1:

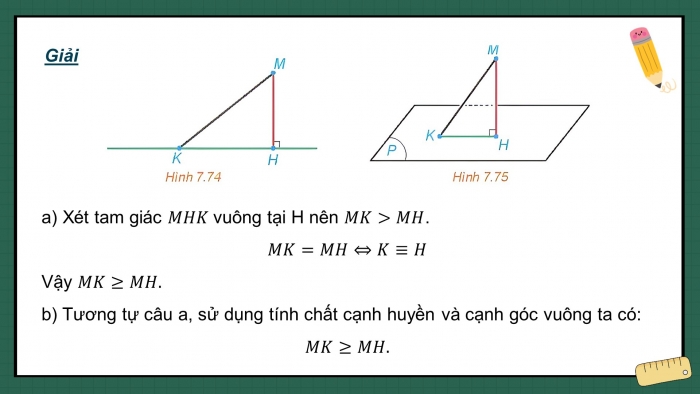
a. Xét tam giác MHK vuông tại H nên MK > MH.

MK = MH ↔ K ≡ H

Vậy MK ≥ MH

b. Tương tự câu a, sử dụng tính chất cạnh huyền và cạnh góc vuông ta có: 

MK  ≥ MH

Kết luận:

- Khoảng cách từ một điểm M đến một đường thẳng a, kí hiệu là d(M,a), là khoảng cách giữa điểm M và hình chiếu H của M trên a.

- Khoảng cách từ một điểm M đến một mặt phẳng (P), kí hiệu d(M, (P)), là khoảng cách giữa M và hình chiếu H của M trên (P).

Chú ý:

d(M,a) = 0 ↔ M ∈ a;

d(M,(P)) = 0↔M ∈ (P)

Nhận xét

- Khoảng cách từ M đến đường thẳng a (mặt phẳng (P)) là khoảng cách nhỏ nhất giữa M và một điểm thuộc a (thuộc (P)).

Chú ý:

Khoảng cách từ đỉnh đến mặt phẳng chứa mặt đáy của hình chóp được gọi là chiều cao của hình chóp đó.

Ví dụ 1:

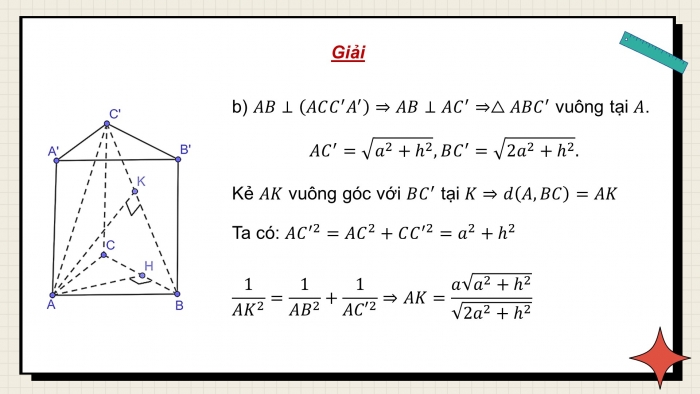
Luyện tập 1:

1. Kẻ AH⊥BC tại H

=> AH ⊥ (BCC’B’) => d(A; (BCC’B’) = AH

Ta có: = +  nên AH =

1. AB⊥ (ACC’A’) => AB⊥AC => ΔABC’ vuông tại A.

AC’ = , BC’ =

Kẻ AH vuông góc với BC’ tại K => d(A; BC) = AK

Ta có: += +

= +  nên AK =

Hoạt động 2. Khoảng cách giữa các đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song

- GV yêu cầu HS thảo luận nhóm đôi, hoàn thành HĐ 2: AM và BN có mối quan hệ gì? MN và AB?

- Từ kết quả trên nhận thấy: Nếu đường thẳng a song song với (P) thì khoảng cách từ các điểm trên a đến (P) như thế nào?

- GV đưa ra câu hỏi: Em hãy nêu định nghĩa khoảng cách giữa các đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song.

- HS thực hiện HĐ 3

- HS suy nghĩ trả lời Câu hỏi (SGK).

Sản phẩm dự kiến:

HĐ 2:

+ Ta có: AM ⊥(P) => AM//BN.

MN//(P) nên mặt phẳng (AMNB) cắt (P) theo giao tuyến AB//MN.

Mặt khác AM⊥ AB

Do đó AMNB là một hình chữ nhật.

Vì AM = BN nên M và N có cùng khoảng cách đến (P).

Kết luận:

Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a kí hiệu là d(a;(P)), là khoảng cách từ một điểm bất kì trên a đến (P).

HĐ 3:

a) Khi một điểm M thay đổi trên đường thẳng m, khoảng cách từ M đến đường thẳng n không thay đổi vì m // n.

b) Vì (P) // (Q) nên các đường thẳng trên mặt (P) đều song song với (Q).

Dựa vào kết quả của hoạt động 2 ta có khi một điểm M thay đổi trên mặt phẳng (P), khoảng cách từ M đến mặt phẳng (Q) không thay đổi. 

Kết luận

- Khoảng cách giữa hai mặt phẳng song song (P) và (Q), kí hiệu d((P); (Q)), là khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia.

- Khoảng cách giữa hai đường đường thẳng song song m và n kí hiệu d(m;n) là khoảng cách từ một điểm thuộc đường thẳng này đến đường thẳng kia.

Câu hỏi:

Lấy M∈ a, M ∈ (P).

a // (Q) nên d(a, (Q)) = d (M, (Q))

1. //(Q) nên d((P), (Q)) = d (M, (Q))

=> d(a, (Q)) = d((P), (Q))

Chú ý. Khoảng cách giữa hai đáy của một hình lăng trụ được gọi là chiều cao của hình lăng trụ đó......

HOẠT ĐỘNG LUYỆN TẬP

Từ nội dung bài học,GV yêu cầu HS hoàn thành các bài tập trắc nghiệm sau:

Câu 1: Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn nửa đường thẳng Ax, By, Cz, Dt cùng phía so với (ABCD) song song với nhau và không nằm trong mặt phẳng (ABCD). Một mặt phẳng (β) lần lượt cắt các nửa mặt phẳng Ax, By, Cz, Dt tại A', B', C', D' thỏa mãn AA' = 2, BB' = 3, CC' = 4. Tính DD'

A. 3

B. 7

C. 2

D. 5

Câu 2: Cho hình chóp S.ABC có $SA\perp (ABC), SA = AB = 2a, tam giác ABC vuông tại B (tham khảo hình vẽ). Khoảng cách từ A đến mặt phẳng (SBC) bằng

A

B. a

C. 2a

D.

Câu 3: Cho hình chóp S.MNPQ có đáy là hình vuông, MN = 3a, với 0<a∈R, biết SM vuông góc với đáy, SM = 6a. Khoảng cách giữa hai đường thẳng NP và SQ bằng

A. 6a

B. 3a

C. 2

D. 3

Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA⊥(ABCD). Gọi I là trung điểm của SC. Khoảng cách từ I đến mặt phẳng (ABCD) bằng độ dài đoạn thẳng nào?

A. IB

B. IC

C. IA

D. IO

Câu 5: Cho hình hộp chữ nhật EFGH.E'F'G'H' có EF = 3a, EH = 4a, EE' = 12a, với 0 < a ∈ R. Khoảng cách giữa hai đường thẳng EF' và GH' bằng

A. 12a

B. 3a

C. 2a

D. 4a

Sản phẩm dự kiến:

HOẠT ĐỘNG VẬN DỤNG

Vận dụng kiến thức, GV yêu cầu HS hoàn thành bài tập sau:

Câu 1: Cho hình lập phương ABCD.A'B'C'D'có cạnh a.

a) Chứng minh rằng hai mặt phẳng (D'AC)và (BC'A') song song với nhau và DB' vuông góc với hai mặt phẳng đó.

b) Xác định các giao điểm E, F của DB' với (D'AC), (BC'A'). Tính d((D'AC), (BC'A')).

Câu 2: Một bể nước có đáy thuộc mặt phẳng nằm ngang. Trong trường hợp này, độ sâu của bể là khoảng cách giữa mặt nước và đáy bể. Giải thích vì sao để đo độ sâu của bể, ta có thể thả quả dọi chạm đáy bể và đo chiều dài của đoạn dây dọi nằm trong bể nước.