Giáo án điện tử Toán 9 chân trời Bài 2: Tiếp tuyến của đường tròn

BÀI 2. TIẾP TUYẾN CỦA ĐƯỜNG TRÒN

CHÀO MỪNG TẤT CẢ HỌC SINH LỚP 9 ĐẾN VỚI BÀI HỌC NGÀY HÔM NAY

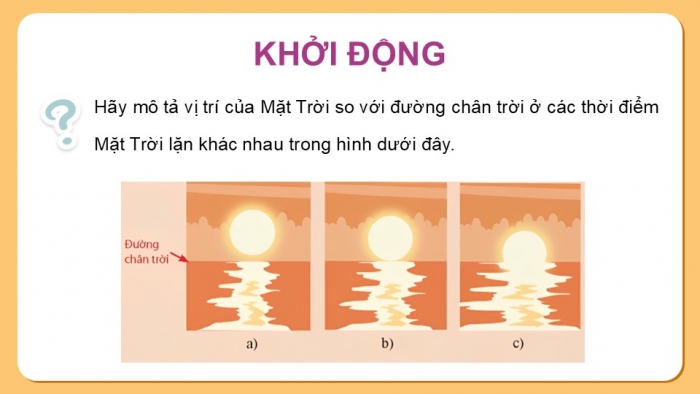
KHỞI ĐỘNG

- GV tổ chức cho HS củng cố lại bài cũ trước khi bước vào nội dung chính của bài học mới.

HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC

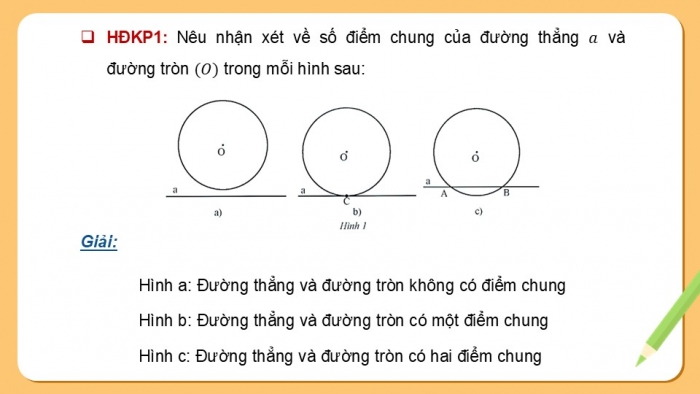
1. VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG TRÒN

Định nghĩa: Nếu đường thẳng a và đường tròn (O):

- Không có điểm chung thì ta nói a và (O) không giao nhau.

- Có duy nhất một điểm chung C thì ta nói a tiếp xúc với (O) tại C, khi đó a là

tiếp tuyến của đường tròn (O) tại C và C là tiếp điểm.

- Có hai điểm chung A, B thì ta nói a cắt (O), a là cát tuyến của đường tròn (O) và A, B là hai giao điểm.

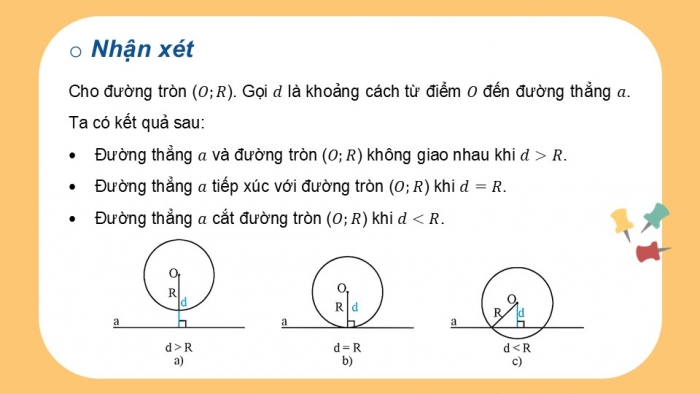
2. DẤU HIỆU NHẬN BIẾT TIẾP TUYẾN ĐƯỜNG TRÒN

Ta có dấu hiệu nhận biết tiếp tuyến của đường tròn: 

Một đường thẳng là tiếp tuyến của đường tròn khi nó đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó.

Ta có các tính chất của tiếp tuyến như sau:

- Tiếp tuyến của đường tròn vuông góc với bán kính tại tiếp điểm.

- Khoảng cách từ tâm của đường tròn đến tiếp tuyến luôn bằng bán kính của đường tròn đó.

3. TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU

Định lí: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:

- Điểm đó cách đều hai tiếp điểm.

- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.

HOẠT ĐỘNG LUYỆN TẬP

Bài 1 trang 88 sgk toán 9 tập 1 ctst

Trong Hình 14, MB, MC lần lượt là tiếp tuyển của đường tròn (O) tại B, C; = 130^o. Tính số đo .

Bài giải:

Ta có COM = COB / 2 = 130^o / 2 = 65^o

=> OMC = 180^o – OCM – COM = 180^o – 90^o – 65^o = 25^o

Mà CMB = 2OMC 

=> CMB = 50^o 

Bài 2 trang 88 sgk toán 9 tập 1 ctst

Quan sát Hình 15. Biết AB, AC lần lượt là tiếp tuyến của đường tròn (O) tại B, C. Tính giá trị của x

Bài giải:

Ta có: 7x – 4 = 3x + 8

=> 7x – 3x = 8 + 4

=> 4x = 12

=> x = 3

Bài 3 trang 89 sgk toán 9 tập 1 ctst

Trong Hình 16, AB = 9, BC = 12, AC = 15 và BC là đường kính của đường tròn (O). Chứng minh AB là tiếp tuyến của đường tròn (O)

Bài giải:

Ta có: AC² = 225

CB² + AB² = 225

=> Tam giác ABC vuông tại B

=> AB là tiếp tuyến của đường tròn  (O; OB)

Bài 4 trang 89 sgk toán 9 tập 1 ctst

Cho tam giác ABC có đường tròn (O) nằm trong và tiếp xúc với ba cạnh của tam giác. Biết AM = 6 cm, BP = 3 cm, CE = 8 cm (HÌnh 17). Tính chu vi tam giác ABC

Bài giải:

Ta có MB = BP

=> MP 3 cm

=> AB = 6 + 3 = 9 cm

Lại có AE = AM 

=> AE = 6 cm

=> AC = 8 + 6 = 14 cm

Mà PC = EC

=> PC = 8 cm

=> BC = 8 + 3 = 11 cm

Vậy chu vi tam giác ABC là: 9 + 14 + 11 = 34 cm

Bài 5 trang 89 sgk toán 9 tập 1 ctst

Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho AC = R. Gọi I là trung điểm của dây AC. Đường thẳng OI cắt tiếp tuyến Ax tại M. Chứng minh rằng:

a) có số đo bằng 90°, từ đó suy ra độ dài của BC theo R;

b) OM là tia phân giác của ;

c) MC là tiếp tuyến của đường tròn (O; R).

Bài giải:

a) Chứng minh ACB có số đo bằng 90°:

Ta có:

- AI = IC (vì I là trung điểm của AC)

- OA = OC = R (vì là bán kính của đường tròn)

Do đó, tam giác AIO và CIO là tam giác cân tại I.

Vậy, góc AIC = góc CIB, và góc AIO = góc CIO.

Từ đó, ta thấy rằng tổng của góc AIC và góc CIO bằng 180°.

Nhưng góc AIO = góc CIO = 90° (vì tiếp tuyến Ax cắt đường tròn tại góc vuông).

Vậy, góc ACB có số đo bằng 90°.

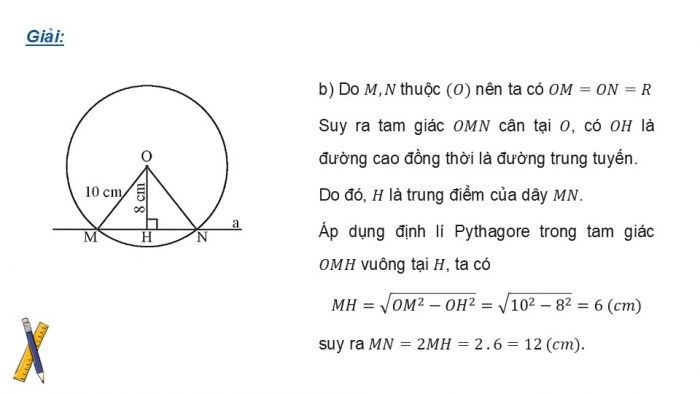
Độ dài của BC theo R:

Khi AC = R, theo định lý Pythagoras, ta có

Với \(AC = R\) và \(AB = 2R\) (vì AB là đường kính của đường tròn), ta có:

b) Chứng minh OM là tia phân giác của COA:

Vì I là trung điểm của AC, nên OI là tia phân giác của góc COA (vì tam giác AOC là tam giác đều, I nằm trên đường trung bình của góc COA).

Vì vậy, OM cũng là tia phân giác của COA.

c) Chứng minh MC là tiếp tuyến của đường tròn (O; R):

Vì OM là tia phân giác của góc COA và OI là tia phân giác của góc COA, nên theo tính chất của tia phân giác, ta có   

Vì OI là đường trung tuyến của tam giác AOC (vì I là trung điểm của AC), nên theo định lý Euclid, MC là tiếp tuyến của đường tròn (O; R).

Sau bài học này em làm được những gì?

Học sinh mô tả được ba vị trí tương đối của đường thẳng và đường tròn (đường thẳng và đường tròn cắt nhau, đường thẳng và đường tròn tiếp xúc nhau, đường thẳng và đường tròn không giao nhau).

Học sinh giải thích được dấu hiệu nhận biết tiếp tuyến của đường tròn và tính chất của hai tiếp tuyến cắt nhau.

Học sinh vận dụng được tính chất tiếp tuyến của đường tròn vào giải toán và giải quyết các tình huống thực tế liên quan đến tiếp tuyến.

HƯỚNG DẪN VỀ NHÀ:

- HS củng cố lại kiến thức, hoàn thành bài tập GV yêu cầu.

- Rèn luyện và nâng cao kĩ năng học tập của bản thân.

- Chuẩn bị trước bài 3 Góc ở tâm, góc nội tiếp.

BÀI HỌC KẾT THÚC, CẢM ƠN CÁC EM ĐÃ LẮNG NGHE!