Giáo án điện tử Toán 12 cánh diều Bài 1: Phương trình mặt phẳng

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC MÔN TOÁN!

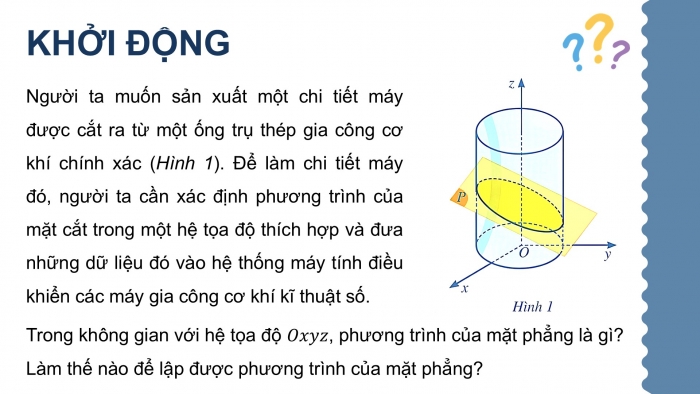
KHỞI ĐỘNG

Người ta muốn sản xuất một chi tiết máy được cắt ra từ một ống trụ thép gia công cơ khí chính xác (Hình 1). Để làm chi tiết máy đó, người ta cần xác định phương trình của mặt cắt trong một hệ tọa độ thích hợp và đưa những dữ liệu đó vào hệ thống máy tính điều khiển các máy gia công cơ khí kĩ thuật số.

Trong không gian với hệ tọa độ , phương trình của mặt phẳng là gì?

Làm thế nào để lập được phương trình của mặt phẳng?

CHƯƠNG V: PHƯƠNG TRÌNH

MẶT PHẲNG, ĐƯỜNG THẲNG,

MẶT CẦU TRONG KHÔNG GIAN

BÀI 1: PHƯƠNG TRÌNH MẶT PHẲNG

NỘI DUNG BÀI HỌC

I. Vectơ pháp tuyến. Cặp vectơ chỉ phương của mặt phẳng

II. Phương trình tổng quát của mặt phẳng

III. Lập phương trình tổng quát của mặt phẳng biết một số điều kiện

IV. Điều kiện song song, vuông góc của hai mặt phẳng

V. Khoảng cách từ một điểm đến một mặt phẳng

VI. Một số ứng dụng của phương trình mặt phẳng trong thực tiễn

I.

VECTƠ PHÁP TUYẾN. CẶP VECTƠ CHỈ PHƯƠNG CỦA MẶT PHẲNG

Cho hình hộp chữ nhật (Hình 2). Giá của vectơ có vuông góc với mặt phẳng hay không?

HĐ1

Giải:

1. Vectơ pháp tuyến

Giá của vectơ là đường thẳng .

Vì là hình hộp chữ nhật nên .

Vậy giá của vectơ vuông góc với mặt phẳng

Khái niệm

Cho mặt phẳng . Nếu vectơ khác và có giá vuông góc với mặt phẳng thì được gọi là vectơ pháp tuyến của mặt phẳng .

Ở hình 3, vectơ là một vectơ pháp tuyến của mặt phẳng .

Nhận xét:

Nếu là vectơ pháp tuyến của một mặt phẳng thì cũng là vectơ pháp tuyến của mặt phẳng đó.

Ví dụ 1: Trong không gian với hệ toạ độ hãy chỉ ra một vectơ pháp tuyến của mặt phẳng

Vectơ có giá là trục và nên là một vectơ pháp tuyến của mặt phẳng

Giải:

LUYỆN TẬP 1

a) Mặt phẳng b) Mặt phẳng

Giải:

a) Vectơ có giá là trục và nên là một vectơ pháp tuyến của mặt phẳng .

b) Vectơ có giá là trục và nên là một vectơ pháp tuyến của mặt phẳng .

Trong không gian với hệ toạ độ , hãy chỉ ra một vectơ pháp tuyến của:

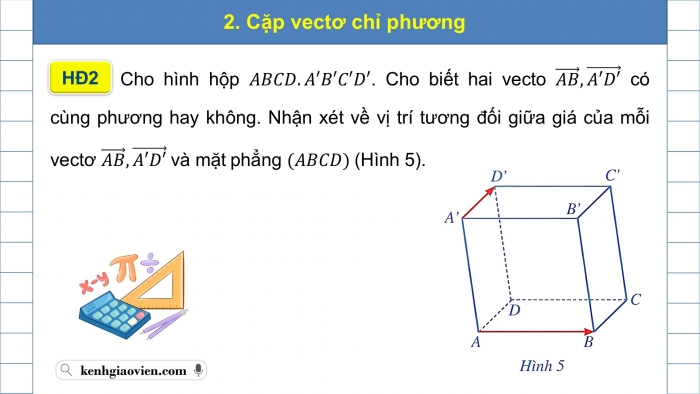
Cho hình hộp . Cho biết hai vecto có cùng phương hay không. Nhận xét về vị trí tương đối giữa giá của mỗi vectơ và mặt phẳng (Hình 5).

HĐ2

2. Cặp vectơ chỉ phương

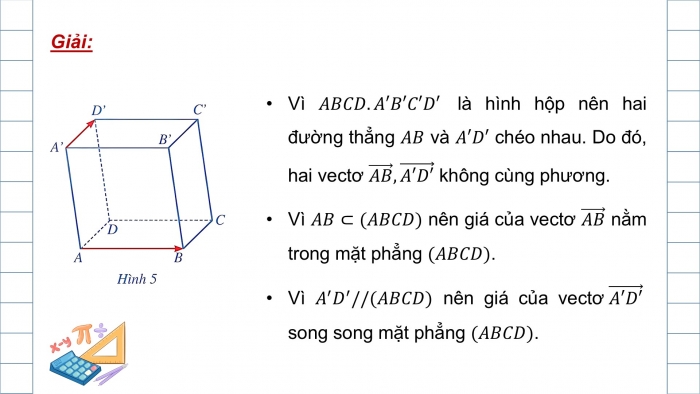
Giải:

• Vì là hình hộp nên hai đường thẳng và chéo nhau. Do đó, hai vectơ không cùng phương.
• Vì nên giá của vectơ nằm trong mặt phẳng .
• Vì nên giá của vectơ song song mặt phẳng .

Kết luận

Cho mặt phẳng . Hai vectơ không cùng phương có giá song song hoặc nằm trong mặt phẳng được gọi là cặp vectơ chỉ phương của mặt phẳng

Ví dụ 2: Quan sát Hình 5.

a) có là cặp vectơ chỉ phương của mặt phẳng hay không? Vì sao?

b) có là cặp vectơ chỉ phương của mặt phẳng hay không? Vì sao?

a) Do hai vectơ không cùng phương và có giá cùng nằm trong mặt phẳng nên là cặp vectơ chỉ phương của mặt phẳng

Giải:

Ví dụ 2: Quan sát Hình 5.

a) có là cặp vectơ chỉ phương của mặt phẳng hay không? Vì sao?

b) có là cặp vectơ chỉ phương của mặt phẳng hay không? Vì sao?

b) Do hai vectơ không cùng phương và có giá cùng song song với mặt phẳng nên là cặp vectơ chỉ phương của mặt phẳng

Giải:

LUYỆN TẬP 2

Trong không gian với hệ toạ độ , hãy chỉ ra một cặp vectơ chỉ phương của mỗi mặt phẳng

Giải:

• Do hai vectơ không cùng phương và có giá cùng nằm trong mặt phẳng nên là cặp vectơ chỉ phương của mặt phẳng .

Giải:

• Do hai vectơ không cùng phương và có giá cùng nằm trong mặt phẳng nên là cặp vectơ chỉ phương của mặt phẳng .
• Do hai vectơ không cùng phương và có giá cùng nằm trong mặt phẳng nên là cặp vectơ chỉ phương của mặt phẳng .

3. Xác định vectơ pháp tuyến của mặt phẳng khi biết cặp vectơ chỉ phương

Cho cặp vectơ chỉ phương của mặt phẳng

HĐ3

a) Hãy chỉ ra toạ độ của một vectơ vuông góc với cả hai vectơ và (Hình 6).

b) Vectơ có là vectơ pháp tuyến của mặt phẳng hay không?

Giải:

a) Xét vectơ có:

Vậy vuông góc với cả hai vectơ và .

b) Vì vuông góc với cả hai vectơ và có nghĩa là giá của nó vuông góc với hai đường thẳng cắt nhau của mặt phẳng .

Suy ra giá của vectơ vuông góc với mặt phẳng .

Mà , do đó vectơ là một vectơ pháp tuyến của mặt phẳng .

Kết luận

Nếu hai vectơ là cặp vectơ chỉ phương của mặt phẳng thì là một vectơ pháp tuyến của mặt phẳng .

Ví dụ 3: Cho mặt phẳng có cặp vectơ chỉ phương là Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng

Một vectơ pháp tuyến của mặt phẳng là:

Giải:

Giải:

LUYỆN TẬP 3

Trong Ví dụ 3, vecto có là vectơ pháp tuyến của mặt phẳng hay không? Vì sao?

Do đó vectơ vuông góc với cả hai vectơ và .

Vậy vectơ cũng là một vectơ pháp tuyến của mặt phẳng .

II.

PHƯƠNG TRÌNH TỔNG QUÁT CỦA MẶT PHẲNG

Trong không gian với hệ toạ độ , cho mặt phẳng đi qua điểm và có vectơ pháp tuyến là

Giả sử là một điểm tuỳ ý thuộc mặt phẳng (Hình 7).

a) Tính tích vô hướng theo

HĐ4

b) Toạ độ của điểm có thoả mãn phương trình: hay không?

Giải:

a) Ta có: .

Khi

.

b) Tọa độ của điểm thỏa mãn phương trình .

Kết luận

Phương trình ( không đồng thời bằng 0) là phương trình tổng quát của mặt phẳng. Hệ số gọi là hệ số tự do của phương trình tổng quát.

Nhận xét

Ta có thể chứng minh được rằng nếu mặt phẳng có phương trình tổng quát là:

Trong đó không đồng thời bằng 0, thì vectơ là một vectơ pháp tuyến của mặt phẳng .

Ví dụ 4: Phương trình nào sau đây là phương trình tổng quát của mặt phẳng?

A. B.

C. D.

Giải:

Ta thấy chỉ có phương trình là phương trình tổng quát của mặt phẳng.

Chọn D.

Ví dụ 5: Chỉ ra một vectơ pháp tuyến của mặt phẳng

Giải:

Ta có:

Mặt phẳng nhận làm vectơ pháp tuyến.

LUYỆN TẬP 4

Chỉ ra một vectơ pháp tuyến của mỗi mặt phẳng sau:

a) ; b)

Giải:

a) Ta có:

Mặt phẳng nhận làm vectơ pháp tuyến.

b) Ta có:

Mặt phẳng nhận làm vectơ pháp tuyến.

III.

LẬP PHƯƠNG TRÌNH TỔNG QUÁT CỦA MẶT PHẲNG BIẾT MỘT SỐ ĐIỀU KIỆN

Cho mặt phẳng đi qua điểm có là vectơ pháp tuyến. Giả sử là một điểm bất kì thuộc mặt phẳng (Hình 9).

a) Tính tích vô hướng

HĐ5

1. Lập phương trình tổng quát của mặt phẳng đi qua một điểm và biết vectơ pháp tuyến

b) Hãy biểu diễn theo ; và

Giải:

a) Ta có: .

Khi .

b) Ta có:

Kết luận

Mặt phẳng đi qua điểm và nhận làm vectơ pháp tuyến có phương trình tổng quát là:

với .

Chú ý:

Mặt phẳng đi qua điểm và nhận làm vectơ pháp tuyến có phương trình là:

--------------------------------------

--------------------- Còn tiếp ----------------------