Giáo án điện tử Toán 12 cánh diều Bài 2: Công thức xác suất toàn phần. Công thức Bayes
Bài giảng điện tử Toán 12 cánh diều. Giáo án powerpoint Bài 2: Công thức xác suất toàn phần. Công thức Bayes. Giáo án thiết kế theo phong cách hiện đại, nội dung đầy đủ, đẹp mắt, tạo hứng thú học tập cho học sinh. Thầy, cô giáo có thể tham khảo.
Xem: => Giáo án toán 12 cánh diều
Click vào ảnh dưới đây để xem 1 phần giáo án rõ nét






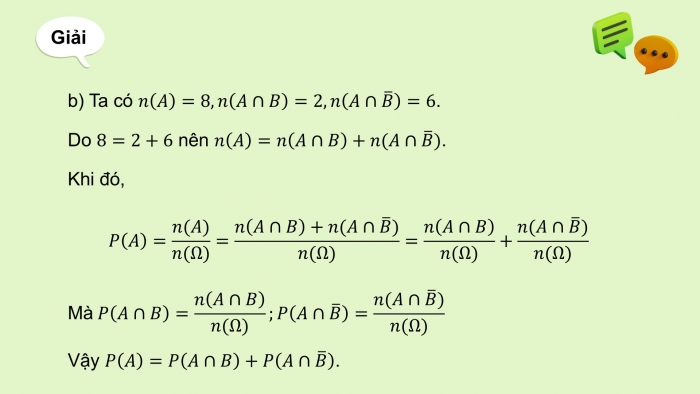
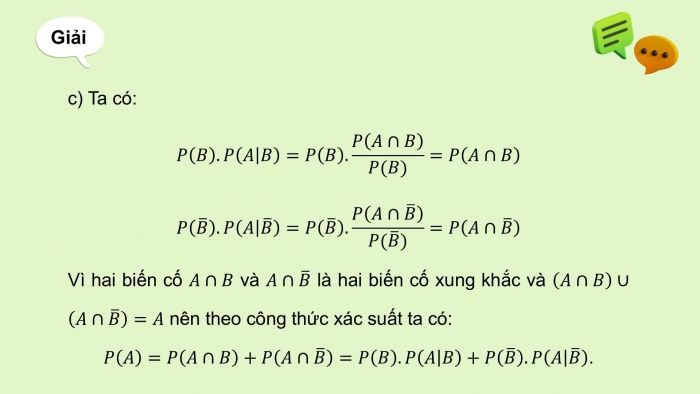


Các tài liệu bổ trợ khác
Xem toàn bộ: Giáo án điện tử toán 12 cánh diều
CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC HÔM NAY!
KHỞI ĐỘNG
Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản phẩm xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%.
Lấy ra ngẫu nhiên một linh kiện từ dây chuyền lắp ráp đó để kiểm tra.
Xác suất để linh kiện được lấy ra đạt tiêu chuẩn là bao nhiêu?
CHƯƠNG VI: MỘT SỐ YẾU TỐ XÁC SUẤT
BÀI 2: CÔNG THỨC XÁC SUẤT TOÀN PHẦN. CÔNG THỨC BAYES
NỘI DUNG BÀI HỌC
CÔNG THỨC XÁC SUẤT TOÀN PHẦN
I
CÔNG THỨC
BAYES
II
I. CÔNG THỨC
XÁC SUẤT TOÀN PHẦN
Một hộp có 24 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, ..., 24; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biến cố : “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố : “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.
HĐ1.
Giải
c) Ta có:
Vì hai biến cố và là hai biến cố xung khắc và nên theo công thức xác suất ta có:
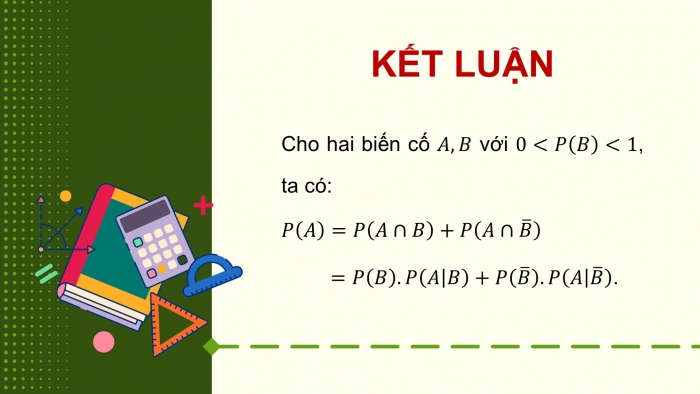
Cho hai biến cố với , ta có:
KẾT LUẬN
Ví dụ 1: Theo một số liệu thống kê, năm 2004 ở Canada có 65% nam giới là thừa cân và 53,4% nữ giới là thừa cân. Nam giới và nữ giới ở Canada đều chiếm 50% dân số cả nước (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics - Understanding why and how, Springer, 2005). Hỏi rằng, trong năm 2004, xác suất để một người Canada được chọn ngẫu nhiên là người thừa cân bằng bao nhiêu?
Xét hai biến cố sau:
: “Người được chọn ra là người thừa cân”;
: “Người được chọn ra là nam giới” (biến cố : “Người được chọn ra là nữ giới”).
Giải
Từ giả thiết ta có:
Theo công thức xác suất toàn phần, ta có:
Vậy xác suất để một người Canada được chọn ngẫu nhiên là người thừa cân bằng
Nói cách khác, tỉ lệ người Canada thừa cân là
Giải
Ví dụ 2: Một hộp có 60 viên bi màu xanh và 40 viên bi màu đỏ; các viên bi có kích thước và khối lượng như nhau. Sau khi thống kê, người ta thấy: 50% số viên bi màu xanh có dán nhãn và 75% số viên bi màu đỏ có dán nhãn; những viên bi còn lại không dán nhãn.
a) Chọn số thích hợp cho trong Bảng 3 (đơn vị: viên bi).
?
b) Lấy ra ngẫu nhiên một viên bi trong hộp. Sử dụng công thức xác suất toàn phần, tính xác suất để viên bi được lấy ra có dán nhãn.
Giải
a) Số viên bi màu đỏ có dán nhãn là: 75% . 40 = 30 (viên bi), không dán nhãn là: 40 - 30 = 10 (viên bi).
Số viên bi màu xanh có dán nhãn là: 50% . 60 = 30 (viên bi), không dán nhãn là: 60 - 30 = 30 (viên bi).
Từ đó, Bảng 3 được hoàn thiện bởi Bảng 4 như sau (đơn vị: viên bi):
Giải
b) Xét hai biến cố sau: : “Viên bi được chọn ra có dán nhãn”; : “Viên bi được chọn ra có màu đỏ”. Khi đó, ta có:
Áp dụng công thức xác suất toàn phần, ta có:
Luyện tập 1. Hãy giải bài toán trong phần mở đầu bằng cách lập bảng thống kê như trong Ví dụ 2, biết rằng cả hai nhà máy sản xuất được 10 000 linh kiện.
Giải
Số linh kiện nhà máy I sản xuất ra là: 55% .10 000 = 5 500 (linh kiện).
Số linh kiện nhà máy II sản xuất ra là: 45% .10 000 = 4 500 (linh kiện).
Số linh kiện nhà máy I sản xuất ra đạt tiêu chuẩn là: 90% . 5 500 = 4 950 (linh kiện), không đạt tiêu chuẩn là: 5 500 – 4 950 = 550 (linh kiện).
Số linh kiện nhà máy II sản xuất ra đạt tiêu chuẩn là: 87% . 4 500 = 3 915 (linh kiện), không đạt tiêu chuẩn là: 4 500 – 3 915 = 585 (linh kiện).
Ta có bảng thống kê như sau:
Giải
Xét hai biến cố:
: “Linh kiện được chọn ra đạt tiêu chuẩn”;
: “Linh kiện được chọn ra do nhà máy I sản xuất”.
Giải
Khi đó, ta có:
Áp dụng công thức xác suất toàn phần, ta có:
Ví dụ 3: Trong trò chơi hái hoa có thưởng của lớp 12A, cô giáo treo 10 bông hoa trên cành cây, trong đó có 5 bông hoa chứa phiếu có thưởng. Bạn Bình hái bông hoa đầu tiên, sau đó bạn An hái bông hoa thứ hai.
a) Vẽ sơ đồ hình cây biểu thị tình huống trên.
b) Từ đó, tính xác suất bạn An hái được bông hoa chứa phiếu có thưởng.
Xét hai biến cố: : “Bông hoa bạn An hái được chứa phiếu có thưởng”
: “Bông hoa bạn Bình hái được chứa phiếu có thưởng”.
Khi đó, ta có:
Giải
a) Sơ đồ hình cây biểu thị tình huống đã cho là:
Giải
b) Áp dụng công thức xác suất toàn phần, ta có:
Giải
Luyện tập 2. Hãy giải bài toán trong phần mở đầu bằng phương pháp sử dụng sơ đồ hình cây như trong Ví dụ 3.
Giải
Xét hai biến cố sau:
: “Linh kiện được chọn ra đạt tiêu chuẩn”;
: “Linh kiện được chọn ra do nhà máy I sản xuất”.
Khi đó, ta có:
Sơ đồ hình cây biểu thị tình huống đã cho là:
Áp dụng công thức xác suất toàn phần, ta có:
Giải
II. CÔNG THỨC
BAYES
Xét hai biến cố trong Hoạt động 1.
HĐ2.
a) Tính: và .
Giải
Với hai biến cố , mà , , ta có:
KẾT LUẬN
Cho hai biến cố với . Do
Nên công thức Bayes còn có dạng:
Nhận xét:
Ví dụ 4: Cho hai biến cố sao cho ; ; . Tính
Giải
Áp dụng công thức Bayes, ta có:
Ví dụ 5: Giả sử có một loại bệnh mà tỉ lệ người mắc bệnh là 0,1%. Giả sử có một loại xét nghiệm, mà ai mắc bệnh khi xét nghiệm cũng có phản ứng dương tính, nhưng tỉ lệ phản ứng dương tính giả là 5% (tức là trong số những người không bị bệnh có 5% số người xét nghiệm lại có phản ứng dương tính).
a) Vẽ sơ đồ hình cây biểu thị tình huống trên.
b) Khi một người xét nghiệm có phản ứng dương tính thì khả năng mắc bệnh của người đó là bao nhiêu phần trăm (làm tròn kết quả đến hàng phần trăm)?
Giải
a) Xét hai biến cố: : “Người được chọn ra không mắc bệnh”;
: “Người được chọn ra có phản ứng dương tính”.
Do tỉ lệ người mắc bệnh là nên
Trong số những người không mắc bệnh có số người có phản ứng dương tính nên .
Vì ai mắc bệnh khi xét nghiệm cũng có phản ứng dương tính nên
Giải
Sơ đồ hình cây ở Hình 2 biểu thị tình huống đã cho.
Giải
b) Ta thấy: Khả năng mắc bệnh của một người xét nghiệm có phản ứng dương tính chính là . Áp dụng công thức Bayes, ta có:
Vậy xác suất mắc bệnh của một người xét nghiệm có phản ứng dương tính là
Luyện tập 3. Cho hai biến cố sao cho ; ; . Tính
Giải
Áp dụng công thức Bayes, ta có:
Luyện tập 4. Được biết có 5% đàn ông bị mù màu, và 0,25% phụ nữ bị mù màu (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics - Understanding why andhow, Springer, 2005). Giả sử số đàn ông bằng số phụ nữ. Chọn một người bị mù màu một cách ngẫu nhiên. Hỏi xác suất để người đó là đàn ông là bao nhiêu?
Giải
Xét hai biến cố sau: : “Người được chọn là đàn ông”;
: “Người được chọn bị mù màu”.
Khi đó, ta có: .
Vì số đàn ông bằng số phụ nữ nên ta có .
Luyện tập 4. Được biết có 5% đàn ông bị mù màu, và 0,25% phụ nữ bị mù màu (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics - Understanding why andhow, Springer, 2005). Giả sử số đàn ông bằng số phụ nữ. Chọn một người bị mù màu một cách ngẫu nhiên. Hỏi xác suất để người đó là đàn ông là bao nhiêu?
Giải
Áp dụng công thức Bayes, ta có:
--------------------------------------
--------------------- Còn tiếp ----------------------
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Giáo án điện tử toán 12 cánh diều
ĐẦY ĐỦ GIÁO ÁN CÁC BỘ SÁCH KHÁC
GIÁO ÁN WORD LỚP 12 CÁNH DIỀU
Giáo án hoạt động trải nghiệm hướng nghiệp 12 cánh diều
Giáo án Tin học 12 - Định hướng khoa học máy tính cánh diều
Giáo án Tin học 12 - Định hướng Tin học ứng dụng cánh diều
GIÁO ÁN POWERPOINT LỚP 12 CÁNH DIỀU
Giáo án Powerpoint Toán 12 Cánh diều
Giáo án powerpoint hình học 12 cánh diều
Giáo án powerpoint đại số 12 cánh diều
Giáo án powerpoint vật lí 12 cánh diều
Giáo án powerpoint sinh học 12 cánh diều
Giáo án powerpoint hoá học 12 cánh diều
Giáo án powerpoint ngữ văn 12 cánh diều
Giáo án powerpoint lịch sử 12 cánh diều
Giáo án powerpoint địa lí 12 cánh diều
Giáo án powerpoint Kinh tế pháp luật 12 cánh diều
Giáo án powerpoint Công nghệ 12 Công nghệ điện - điện tử cánh diều
Giáo án powerpoint Công nghệ 12 Lâm nghiệp - Thuỷ sản cánh diều
Giáo án powerpoint Tin học 12 - Định hướng Tin học ứng dụng cánh diều
Giáo án powerpoint Tin học 12 - Định hướng khoa học máy tính cánh diều
Giáo án powerpoint hoạt động trải nghiệm hướng nghiệp 12 cánh diều
GIÁO ÁN CHUYÊN ĐỀ LỚP 12 CÁNH DIỀU
GIÁO ÁN POWERPOINT CHUYÊN ĐỀ 12 CÁNH DIỀU
GIÁO ÁN DẠY THÊM LỚP 12 CÁNH DIỀU
Giáo án dạy thêm toán 12 cánh diều
Giáo án dạy thêm ngữ văn 12 cánh diều
Giáo án powerpoint dạy thêm ngữ văn 12 cánh diều
Giáo án powerpoint dạy thêm toán 12 cánh diều
