Giáo án điện tử Toán 12 cánh diều Bài 4: Ứng dụng hình học của tích phân
Bài giảng điện tử Toán 12 cánh diều. Giáo án powerpoint Bài 4: Ứng dụng hình học của tích phân. Giáo án thiết kế theo phong cách hiện đại, nội dung đầy đủ, đẹp mắt, tạo hứng thú học tập cho học sinh. Thầy, cô giáo có thể tham khảo.
Xem: => Giáo án toán 12 cánh diều
Click vào ảnh dưới đây để xem 1 phần giáo án rõ nét








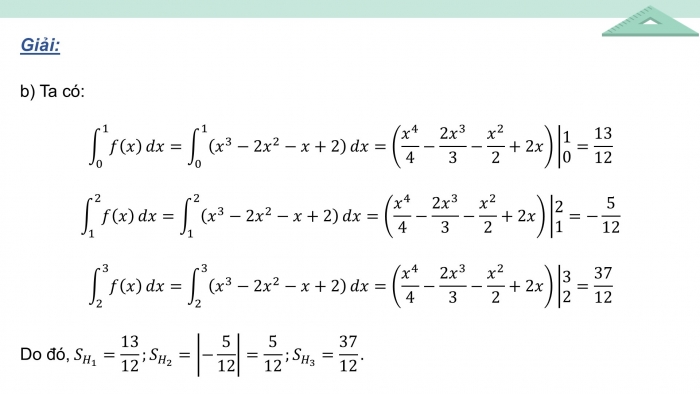
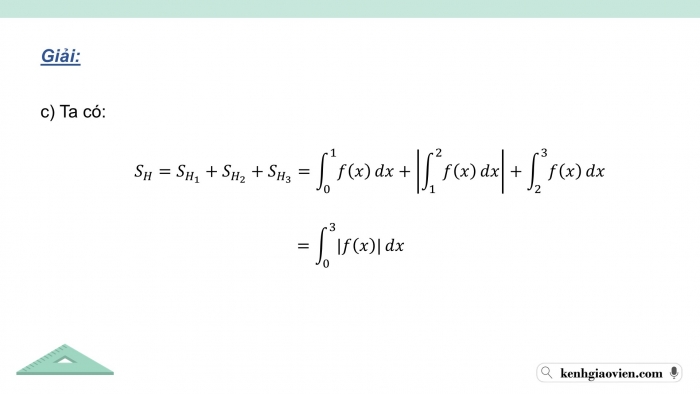


Các tài liệu bổ trợ khác
Xem toàn bộ: Giáo án điện tử toán 12 cánh diều
CHÀO MỪNG CẢ LỚP ĐẾN VỚI TIẾT HỌC HÔM NAY!
KHỞI ĐỘNG
Gốm Bát Tràng là tên gọi chung của các loại đồ gốm Việt Nam được sản xuất tại làng Bát Tràng, thuộc xã Bát Tràng, huyện Gia Lâm, Hà Nội. Với hơn 700 năm tuổi, gốm Bát Tràng nổi tiếng ở trong và ngoài nước về chất lượng gốm và độ tinh xảo của các sản phẩm.
Những chiếc chén trong bộ ấm chén uống trà ở Hình 10 có dạng khối tròn xoay. Thể tích của các khối tròn xoay được tính như thế nào?
CHƯƠNG IV:
NGUYÊN HÀM. TÍCH PHÂN
BÀI 4: ỨNG DỤNG
HÌNH HỌC CỦA TÍCH PHÂN
NỘI DUNG BÀI HỌC
I. Tính diện tích hình phẳng
II. Tính thể tích của hình khối
I.
TÍNH DIỆN TÍCH
HÌNH PHẲNG
Cho hàm số có đồ thị minh họa ở Hình 11.
a) Quan sát Hình 11, hãy cho biết các hình phẳng , lần lượt được giới hạn bởi các đường thẳng và đồ thị hàm số nào.
b) Tính diện tích , , của các hình phẳng đó.
1. Diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng .
HĐ1
c) Gọi là hợp của cac hình phẳng . Hình phẳng được gọi là hình phẳng giới hạn bởi đồ thị hàm số trục hoành và các đường thẳng . Chứng tỏ rằng diện tích của hình phẳng bằng
1. Diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng .
HĐ1
Giải:
a) Quan sát Hình 11, ta thấy:
- Hình phẳng được giới hạn bởi các đường thẳng , trục và đồ thị hàm số .
- Hình phẳng được giới hạn bởi các đường thẳng , trục và đồ thị hàm số .
- Hình phẳng được giới hạn bởi các đường thẳng , trục và đồ thị hàm số .
Giải:
b) Ta có:
Giải:
c) Ta có:
Kết luận
Cho hàm số liên tục trên đoạn . Khi đó, diện tích của hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng là:
Ví dụ 1: Cho hàm số có đồ thị như Hình 12.
Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số , trục và hai đường thẳng
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số , trục và hai đường thẳng là:
Giải:
Luyện tập 1
Trong Hình 13, tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số , trục và hai đường thẳng
Giải:
Ta có:
Cho các hàm số và
2. Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số , và hai đường thẳng .
HĐ2
Gọi là diện tích hình phẳng giới hạn bởi trục , hai đường thẳng và đồ thị hàm số .
Gọi là diện tích hình phẳng giới hạn bởi trục , hai đường thẳng và đồ thị hàm số .
Gọi là diện tích hình phẳng giới hạn bởi các đồ thị hàm số và hai đường thẳng (Hình 14).
a) Biểu diễn theo .
b) So sánh và .
Giải:
a) Quan sát Hình 14, ta thấy
b) Ta có:
Khi đó
Vậy
Kết luận
Cho các hàm số liên tục trên đoạn . Khi đó, diện tích hình phẳng giới hạn bởi đồ thị của các hàm số và hai đường thẳng là:
Ví dụ 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số , và hai đường thẳng
Diện tích hình phẳng đã cho là:
Giải:
Ví dụ 3: Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số , và hai đường thẳng .
Ta có: với mọi (Hình 15). Vậy diện tích hình phẳng đó là:
Giải:
Luyện tập 2
Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số và hai đường thẳng
Giải:
Ta có: với mọi .
Ví dụ 4: Trên cửa sổ có dạng hình chữ nhật, hoạ sĩ thiết kế logo hình con cá cho một doanh nghiệp kinh doanh hải sản. Logo là hình phẳng giới hạn bởi hai parabol với các kích thước được cho trong Hình 16 (đơn vị trên mỗi trục toạ độ là decimét). a) Lập phương trình các parabol và
b) Tính diện tích của logo.
c) Logo chỉ cho phép 50% lượng ánh sáng đi qua. Lượng ánh sáng đi qua toàn bộ cửa sổsau khi làm logo sẽ giảm bao nhiêu phần trăm (làm tròn kết quả đến hàng phần mười)?
Giải:
a) Giả sử parabol cho bởi Do parabol đi qua điểm nên , suy ra
Vì parabol đi qua các điểm nên ta có:
Giải:
Giả sử parabol cho bởi Do parabol đi qua điểm nên , suy ra
Vì parabol đi qua các điểm nên ta có:
Giải:
b) Diện tích của logo là: , trong đó là diện tích hình phẳng giới hạn bởi các parabol và hai đường thẳng là diện tích hình phẳng giới hạn bởi các parabol và hai đường thẳng
Do đó, ta có:
Giải:
Giải:
c) Gọi là lượng ánh sáng đi qua mỗi của logo.
Mặt khác, diện tích của cửa sổ là và lượng ánh sáng đi qua mỗi của phần cửa sổ nằm ngoài logo là .
Suy ra, lượng ánh sáng đi qua cửa sổ trước khi làm logo là và lượng ánh sáng đi qua phần cửa sổ nằm ngoài logo là:
Giải:
Do đó, tổng lượng ánh sáng đi qua cửa sổ sau khi làm logo là:
Tỉ số phần trăm của lượng ánh sáng đi qua cửa sổ sau khi làm logo so với lượng ánh sáng đi qua cửa sổ trước khi làm logo là:
Vậy lượng ánh sáng khi đi qua toàn bộ cửa sổ sau khi làm logo sẽ giảm đi xấp xỉ là:
II.
TÍNH THỂ TÍCH HÌNH KHỐI
kenhgiaovien
- Bài giảng và giáo án này chỉ có duy nhất trên kenhgiaovien.com
- Bất cứ nơi nào đăng bán lại đều là đánh cắp bản quyền và hưởng lợi bất chính trên công sức của giáo viên.
- Vui lòng không tiếp tay cho hành vi xấu.
Zalo: 0386 168 725
Cắt khối lập phương có cạnh bằng 1 bởi một mặt phẳng tuỳ ý vuông góc với trục tại , với ta nhận được hình phẳng có diện tích là (Hình 17).
a) Tính
b) So sánh thể tích khối lập phương đó với .
1. Thể tích của vật thể
HĐ3
1. Thể tích của vật thể
Giải:
a) Ta có: .
b) Thể tích khối lập phương là .
Ta có:
Vậy Thể tích khối lập phương đó bằng .
Cắt một vật thể bởi hai mặt phẳng vuông góc với trục tại và (). Một mặt phẳng tùy ý vuông góc với tại cắt vật thể đó theo hình phẳng có diện tích là . Giả sử hàm số liên tục trên . Khi đó, thể tích của phần vật thể giới hạn bởi hai mặt phẳng trên được tính bởi công thức
Định lí
Chú ý: Nếu không đổi với mỗi thì .
Ví dụ 5: Tính thể tích khối lăng trụ, biết diện tích đáy bằng và chiều cao bằng .
Giải:
Chọn trục song song với đường cao của khối lăng trụ, còn hai đáy nằm trong hai mặt phẳng vuông góc với tại và (Hình 19).
Khi đó, một mặt phẳng vuông góc với trục , cắt lăng trụ theo hình phẳng có diện tích không đổi với mỗi Áp dụng chú ý trên, ta có:
Luyện tập 3
Cắt một vật thể bởi hai mặt phẳng vuông góc với trục tại và . Một mặt phẳng tuỳ ý vuông góc với tại cắt vật thể đó theo hình phẳng có diện tích là . Tính thể tích của phần vật thể được giới hạn bởi hai mặt phẳng trên.
Giải:
Ví dụ 6: Cho khối chóp có chiều cao bằng và diện tích đáy bằng Chọn trục vuông góc với mặt phẳng đáy tại điểm sao cho gốc trùng với đỉnh của khối chóp và có hướng xác định bởi vectơ (minh hoạ ở Hình 20). Khi đó . Một mặt phẳng vuông góc với trục tại cắt khối chóp theo hình phẳng có diện tích . Người ta chứng minh được rằng Tính thể tích
khối chóp đó.
Giải:
Thể tích khối chóp đó là:
Nhận xét:
- Cho khối lăng trụ có chiều cao bằng và diện tích đáy bằng . Thể tích của khối lăng trụ đó được tính bởi công thức .
- Cho khối chóp có chiều cao bằng và diện tích đáy bằng . Thể tích của khối chóp đó được tính bởi công thức
Luyện tập 4
Cho khối chóp cụt đều tạo bởi khối chóp đỉnh , diện tích hai đáy lần lượt là và chiều cao . Chọn trục chứa đường cao của khối chóp và gốc trùng với đỉnh (Hình 21). Hai mặt phẳng đáy của khối chóp cụt đều lần lượt cắt tại và . Đặt Một mặt phẳng vuông góc với trục tại cắt khối chóp cụt đều theo hình phẳng có diện tích .
Tính thể tích khối chóp cụt đều đó.
Giải:
Ví dụ 7: Cô Hạnh đổ bê tông một đường đi trong vườn (phần được tô màu) với kích thước được cho trong Hình 22. Biết rằng đường cong được cho bởi đồ thị của một hàm số liên tục và đường cong nhận được từ đường cong bằng cách tịnh tiến theo phương thẳng đứng lên phía trên 2 m.
Ngoài ra, cô Hạnh quyết định đồ lớp bê tông dày 15 cm và giá tiền 1 bê tông là 1 080 000 đồng. Tính số tiền cô Hạnh cần dùng để đổ bê tông con đường đó.
Giải:
Xét hệ trục toạ độ như Hình 23 (đơn vị trên mỗi trục toạ độ là mét).
Trong hệ trục toạ độ đó, đường cong được cho bởi đồ thị của hàm số liên tục . Suy ra, đường cong được cho bởi đồ thị của hàm số liên tục .
Áp dụng công thức tính diện tích, ta có:
Giải:
Do đó, thể tích khối bê tông dùng để đổ con đường là:
Vậy số tiền cô Hạnh cần dùng để đổ bê tông con đường đó là:
(đồng).
Xét nửa hình tròn tâm , bán kính (Hình 24). Nửa hình tròn đó là hình phẳng giới hạn bởi trục và đồ thị hàm số
a) Tìm hàm số
b) Quay nửa hình tròn đó quanh trục hoành, ta nhận được hình cầu tâm bán kính (Hình 25). Xét điểm nằm trên nửa đường tròn tâm bán kính Gọi là hình chiếu của điểm trên trục . Khi quay nửa hình tròn quanh trục hoành, đoạn thẳng tạo nên một hình tròn tâm bán kính . Tính diện tích của hình tròn đó theo .
2. Thể tích của khối tròn xoay
HĐ4
Từ đó, sử dụng công thức tính thể tích vật thể, hãy tính thể tích của hình cầu tâm bán kính .
Giải:
a) Hàm số chính là phương trình của nửa đường tròn tâm , bán kính .
Ta có phương trình đường tròn tâm , bán kính là .
Suy ra
b) Hình tròn tâm bán kính có diện tích là .
Thể tích của hình cầu tâm bán kính là:
Tổng quát
Ta có định lí sau: Hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng quay quanh trục tạo thành một khối tròn xoay có thể tích bằng
Cho hàm số liên tục, không âm trên đoạn . Hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng khi quay quanh trục tạo thành một hình khối gọi là khối tròn xoay. Khi cắt khối tròn xoay đó bởi một mặt phẳng vuông góc với trục , ta được một hình tròn có bán kính là .
Ví dụ 8: Cho hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng . Tính thể tích khối tròn xoay tạo thành khi cho hình phẳng đó quay quanh trục .
Giải:
Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng , quay quanh trục là:
Luyện tập 5
Cho hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng Tính thể tích khối tròn xoay tạo thành khi cho hình phẳng đó quay quanh trục
Giải:
Ví dụ 9: Xét chiếc chén trong bộ ấm chén uống trà ở phần mở đầu, bạn Dương ước lượng được rằng chiếc chén được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng quay quanh trục (đơn vị trên mỗi trục toạ độ là centimét) (Hình 27). Tính thể tích của chiếc chén (làm tròn đến hàng đơn vị của centimét khối).
Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số
trục hoành và hai đường thẳng quay quanh trục là:
Vậy thể tích của chiếc chén khoảng .
Giải:
LUYỆN
TẬP
--------------------------------------
--------------------- Còn tiếp ----------------------
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Giáo án điện tử toán 12 cánh diều
ĐẦY ĐỦ GIÁO ÁN CÁC BỘ SÁCH KHÁC
GIÁO ÁN WORD LỚP 12 CÁNH DIỀU
Giáo án hoạt động trải nghiệm hướng nghiệp 12 cánh diều
Giáo án Tin học 12 - Định hướng khoa học máy tính cánh diều
Giáo án Tin học 12 - Định hướng Tin học ứng dụng cánh diều
GIÁO ÁN POWERPOINT LỚP 12 CÁNH DIỀU
Giáo án Powerpoint Toán 12 Cánh diều
Giáo án powerpoint hình học 12 cánh diều
Giáo án powerpoint đại số 12 cánh diều
Giáo án powerpoint vật lí 12 cánh diều
Giáo án powerpoint sinh học 12 cánh diều
Giáo án powerpoint hoá học 12 cánh diều
Giáo án powerpoint ngữ văn 12 cánh diều
Giáo án powerpoint lịch sử 12 cánh diều
Giáo án powerpoint địa lí 12 cánh diều
Giáo án powerpoint Kinh tế pháp luật 12 cánh diều
Giáo án powerpoint Công nghệ 12 Công nghệ điện - điện tử cánh diều
Giáo án powerpoint Công nghệ 12 Lâm nghiệp - Thuỷ sản cánh diều
Giáo án powerpoint Tin học 12 - Định hướng Tin học ứng dụng cánh diều
Giáo án powerpoint Tin học 12 - Định hướng khoa học máy tính cánh diều
Giáo án powerpoint hoạt động trải nghiệm hướng nghiệp 12 cánh diều
GIÁO ÁN CHUYÊN ĐỀ LỚP 12 CÁNH DIỀU
GIÁO ÁN POWERPOINT CHUYÊN ĐỀ 12 CÁNH DIỀU
GIÁO ÁN DẠY THÊM LỚP 12 CÁNH DIỀU
Giáo án dạy thêm toán 12 cánh diều
Giáo án dạy thêm ngữ văn 12 cánh diều
Giáo án powerpoint dạy thêm ngữ văn 12 cánh diều
Giáo án powerpoint dạy thêm toán 12 cánh diều
